Механические модели

Вязкоупругие свойства тел (сочетание вязкого течения и высокой эластичности) моделируются системами, состоящими из различных комбинаций двух простых элементов: 1) пружины (упругий элемент) и 2) поршня с отверстиями, движущегося в цилиндре с вязкой жидкостью (вязкий элемент). Эти элементы и «конструируемые» с их помощью модели показаны на рис. 6.19 слева. Справа показаны зависимости деформации (ε) от времени при импульсном воздействии внешней силы: в момент времени t = 0 к телу, поведение которого моделируется, прикладывается постоянная сила F; в момент времени t₁ действие силы прекращается.

Моделью упругого тела является пружина (рис. 6.19, а), подчиняющаяся закону Гука. Деформация (ε) мгновенно появляется в момент t = 0 и мгновенно исчезает в момент t₁.

Моделью вязкого тела является поршень с отверстиями, движущийся в цилиндре с вязкой жидкостью (рис. 6.19, б). Связь между скоростью деформации вязкой среды (скоростью перемещения поршня) и напряжением имеет вид

Модель Максвелла

В модели Максвелла упругий и вязкий элементы соединены последовательно (рис. 6.19, в). Напряжение в каждом элементе является

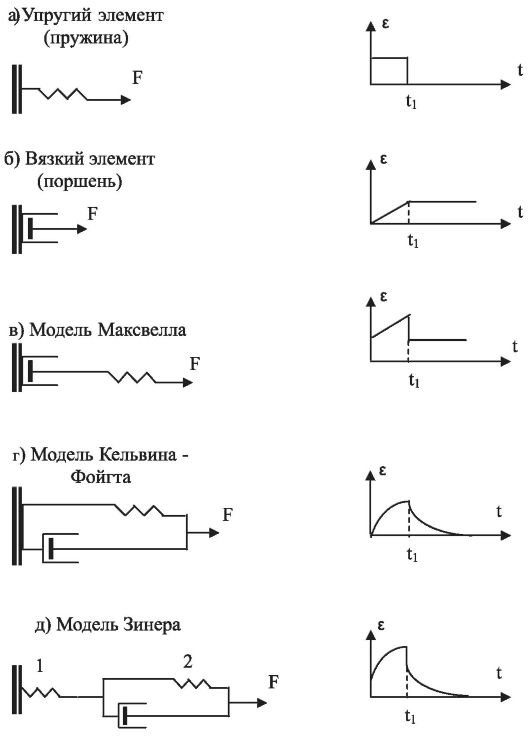Рис. 6.19. Механические модели вязкоупругих тел и динамика развития деформации

одинаковым. В любой момент времени для деформации выполняется условие

Решение этого уравнения приводит к следующему характеру развития деформации. В момент t = 0 пружина мгновенно растягивается, а затем начинается линейное нарастание деформации, связанное с движением поршня. В момент t₁ пружина сокращается до начального размера, а поршень останавливается - имеет место остаточная деформация.

С помощью модели Максвелла можно моделировать следующие механические процессы.

Релаксация напряжения в материале: ε = const, dε/dt = 0, т.е. поддерживается постоянная деформация. В этом случае из уравнения (6.10) следует

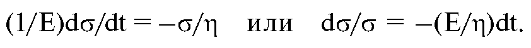Интегрируя последнее выражение от начального момента времени и начального напряжения σ _о до текущих значений t иσ, получаем выражение, описывающее изменение напряжения со временем, т.е. релаксацию напряжения:

т.е. под действием постоянной приложенной силы происходит вязкое течение (поршень движется с постоянной скоростью).

При изучении свойств волос используют явление релаксации напряжения в них. Этот процесс аппроксимируют моделью, состоящей из 4 параллельно соединенных моделей Максвелла.

Дата добавления: 2014-01-03