Генеральная дисперсия

Для того чтобы охарактеризовать рассеяние значений количественного признака Х генеральной совокупности вокруг своего среднего значения, вводят сводную характеристику — генеральную дисперсию.

Генеральной дисперсией D_г называют среднее арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения.

Если все значения признака генеральной совокупности объема N различны, то

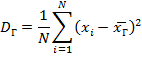
Если же значения признака имеют соответственно частоты N₁, N₂, …, N_k, где N₁ +N₂+…+N_k= N, то

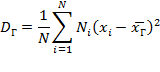
Кроме дисперсии для характеристики рассеяния зна­чений признака генеральной совокупности вокруг своего среднего значения пользуются сводной характеристикой — средним квадратическим отклонением.

Генеральным средним квадратическим отклонением (стандартом) называют квадратный корень из генеральной дисперсии: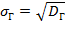

4) Выборочная дисперсия.

Для того, чтобы наблюдать рассеяние количественного признака значений выборки вокруг своего среднего значения, вводят сводную характеристику - выборочную дисперсию.

Выборочной дисперсией называют среднее арифметическое квадратов отклонения наблюдаемых значений признака от их среднего значения.

Если все значения признака выборки различны, то

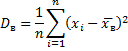
если же все значения имеют частоты n₁, n₂,…,n_k, то

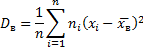
Для характеристики рассеивания значений признака выборки вокруг своего среднего значения пользуются сводной характеристикой - средним квадратическим отклонением.

Выборочным средним квадратическим отклоненим называют квадратный корень из выборочной дисперсии: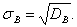

Так же, как в теории случайных величин, можно доказать, что справедлива следующая формула для вычисления выборочной дисперсии: .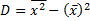

Пример 1. Найдем числовые характеристики выборки, заданной статистическим рядом

xi
ni

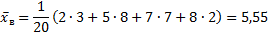
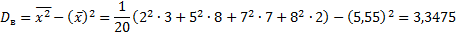
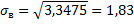
Замечание 1: если выборка представлена интервальным вариационным рядом, то за x_i принимают середины частичных интервалов.

Замечание 2. Если первоначальные варианты большие числа, то целесообразно вычесть из всех вариант одно и то же число С, равное выборочной средней или близкое к ней, т. е. перейти к условным вариантам u_i=x_i-C (дисперсия при этом не изменится). Тогда

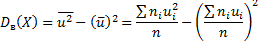
Замечание 3. Если первоначальные варианты являются десятичными дробями с k десятичными знаками после запятой, то, чтобы избежать действий с дробями, умножают первоначальные ва­рианты на постоянное число С =10 ^k, т. е. переходят к условным вариантам u_i=Cx_i. При этом дисперсия увеличится в С² раз. Поэтому, найдя дисперсию условных вариант, надо разделить ее на С²:

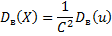
Дата добавления: 2014-01-03