Шкала измерений, принципы и методы измерений

Классификация измерений.

Измерения различают

по способу получения информации,

по характеру из­менений измеряемой величины в процессе измерений,

по количеству измеритель­ной информации,

по отношению к основным единицам.

Классификация измерений изображена на схеме.

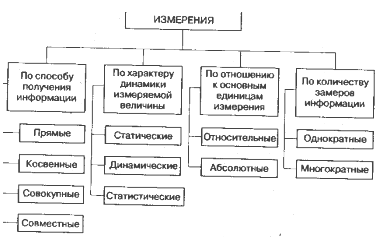
Схема 3. Классификация измерений

По способу получения информации измерения разделяют на прямые, косвенные, совокупные и совместные.

Прямые измерения — это непосредственное сравнение физической величи­ны с ее мерой. Например, при определении длины предмета линейкой происхо­дит сравнение искомой величины (количественного выражения значения длины) с мерой, т.е. линейкой.

Косвенные измерения отличаются от прямых тем, что искомое значение ве­личины устанавливают по результатам прямых измерений таких величин, которые связаны с искомой определенной зависимостью. Так, если измерить силу тока ам­перметром, а напряжение вольтметром, то по известной функциональной взаимо­связи всех трех названных величин можно рассчитать мощность электрической цепи.

Совокупные измерения сопряжены с решением системы уравнений, составляемых по результатам одновременных измерений нескольких однородных величин. Решение системы уравнений дает возможность вычислить искомую величину.

Совместные измерения — это измерения двух или более неоднородных фи­зических величин для определения зависимости между ними.

Совокупные и совместные измерения часто применяют в измерениях различ­ных параметров и характеристик в области электротехники.

По характеру изменения измеряемой величины в процессе измерений бывают статистические, динамические и статические измерения.

Статистические измерения связаны с определением характеристик случай­ных процессов, звуковых сигналов, уровня шумов и т.д.

Статические измерения имеют место тогда, когда измеряемая величина практически постоянна.

Динамические измерения связаны с такими величинами, которые в процессе измерений претерпевают те или иные изменения.

Статические и динамические измерения в идеальном виде на практике редки.

По количеству измерительной информации различают одно­кратные и многократные измерения.

Однократные измерения — это одно измерение одной величины, т.е. число измерений равно числу измеряемых величин. Практическое применение такого вида измерений всегда сопряжено с большими погрешностями, поэтому следует проводить не менее трех однократных измерений и находить конечный результат как среднее арифметическое значение.

Многократные измерения характеризуются превышением числа измерений количества измеряемых величин. Обычно минимальное число измерений в данном случае больше трех. Преимущество многократных измерений в значительном снижении влияний случайных факторов на погрешность измерения.

Абсолютными измерениями называют такие, при которых используются прямое измерение одной (иногда нескольких) основной величины и физическая константа. Так, в известной формуле Эйнштейна Е=тс² масса (т) — основная физическая величина, которая может быть измерена прямым путем (взвешиванием), а скорость света (с) — физическая константа.

Относительные измерения базируются на установлении отношения изме­ряемой величины к однородной, применяемой в качестве единицы. Естественно, что искомое значение зависит от используемой единицы измерений.

Основные величины не зависимы друг от друга, но они могут служить основой для установления связей с другими физическими величинами, которые называют производными от них. Основным величинам соответствуют основные единицы измерений, а производ­ным — производные единицы измерений.

Совокупность основных и производных единиц называется системой единиц физических величин.

Наиболее широко распространена во всем мире Международная система единиц СИ. Международная система СИ считается наиболее совершенной и универсаль­ной по сравнению с предшествовавшими ей.

В зависимости от использованных средств измерений измерения классифицируют как технические и метрологические.

Технические измерения- измерения с помощью рабочих средств измерений.

Метрологические измерения- измерения при помощи этало­нов и образцовых средств измерений с целью воспроизведения единиц физических величин для передачи их размера рабочим средствам измерений

С измерениями связаны такие понятия, как "шкала измерений", "принцип измерений", "метод измерений".

Шкала измерений — это упорядоченная совокупность значений физической величины, которая служит основой для ее измерения. Поясним это понятие на примере температурных шкал.

В шкале Цельсия за начало отсчета принята температура таяния льда, а в качестве основного интервала (опорной точки) — температура кипения воды. Одна сотая часть этого интервала является единицей температуры (градус Цельсия). В температурной шкале Фаренгейта за начало отсчета принята температура тая­ния смеси льда и нашатырного спирта (либо поваренной соли), а в качестве опорной точки взята нормальная температура тела здорового человека. За едини­цу температуры (градус Фаренгейта) принята одна девяносто шестая часть ос­новного интервала. По этой шкале температура таяния льда равна + 32°F, а тем­пература кипения воды + 212°F. Таким образом, если по шкале Цельсия раз­ность между температурой кипения воды и таяния льда составляет 100°С, то по Фаренгейту она равна 180°F. На этом примере мы видим роль принятой шкалы как в количественном значении измеряемой величины, так и в аспекте обеспече­ния единства измерений. В данном случае требуется находить отношение разме­ров единиц, чтобы можно было сравнить результаты измерений.

Таким образом, понятие шкала используется в математиче­ском смысле, т. е. как метод оценивания и сопоставления свойств различных объектов. В метрологической практике известны несколько разновидностей шкал: шкала наименований, шкала порядка, шкала интервалов, шкала отношений и др.

Шкала порядка - это такой метод оценивания, при котором оцениваемые параметры, показатели или иные объекты оценивания располагаются в порядке увеличения или уменьшения значения па­раметра (показателя) или свойств объекта, причем способ определе­ния порядка расположения не связан с какой-либо численной харак­теристикой оцениваемых объектов.

Характеристика значений измеряемой величины дается в баллах (шкала землетрясений, силы ветра, твердости физических тел и т.п.).

Классическим примером оцени­вания с применением шкалы порядка является оценивание твердости минералов на основе шкалы Мооса. Шкала Мооса относитель­ной твердости минералов состоит из 10 эталонов твердости: тальк -1, гипс- 2, кальцит- 3, флюорит- 4, апатит- 5, ортоклаз- 6, кварц- 7, топаз- 8, корунд- 9, алмаз- 10. Относительная твер­дость определяется путем царапанья эталоном шкалы Мооса по­верхности испытываемого объекта. Если эталон, имеющий твер­дость п, п= 1, 2,..., 10, царапает исследуемый образец, а исследуе­мый образец царапает эталон с твердостью п - 1, то твердость ми­нерала принимается равной (п- 1), 5. В рассмотренном примере оценивание в шкале порядка обусловлено тем фактом, что для оце­нивания исследуемого свойства не существует метода, позволяю­щего осуществить оценку в установленных единицах измерения.

Другим примером применения шкалы порядка может служить оценка качества продукции, при которой учитывается несколько свойств. В этом случае качество характеризуется вектором, коор­динатами которого являются показатели свойств, учитываемых при оценке. Поэтому в этом случае для получения имеющей смысл оценки необходимо создать некую шкалу, аналогичную шкале Мооса.

Шкала интервалов- это такой метод оценивания, при кото­ром существенной характеристикой является разность между зна­чениями оцениваемых параметров, которая может быть выражена числом установленных в этой шкале единиц. При этом начало от­счета может быть установлено произвольно. Примером шкалы ин­тервалов может служить шкала температур, времени, длины.

Шкала отношений- это такой метод оценивания, при кото­ром используется единица измерения и, следовательно, величина оцениваемого параметра может быть представлена в виде

Q = qN,

где Q - величина оцениваемого параметра, q - единица измерения,

N - положительное действительное число, являющееся коли­чественной характеристикой этого параметра.

Шкала отношений имеет естественное нулевое значение, а единица измерений устанавливается по согласованию. Например, шкала массы (обычно мы говорим "веса"), начинаясь от нуля, может быть градуирована по-разному в зависимости от требуемой точности взвешивания. Сравните бытовые и аналитические весы.

В шкале порядка возможны логические операции, но невоз­можны арифметические действия. Если значение параметра про­дукции, измеряемого в шкале порядка, у первого вида продукции больше, чем у второго, а у третьего больше, чем у первого, то можно сделать вывод о том, что значение этого параметра у третьего вида продукции больше, чем у второго. Однако в обоих случаях нельзя сказать, насколько больше. Это можно сделать, если для измерения параметра может быть применена шкала ин­тервалов. На отградуированной шкале может быть определена разность между любыми двумя значениями параметра. Но как в шкале интервалов, так и, тем более, в шкале порядка нельзя оп­ределить, во сколько раз значение одного параметра больше, чем значение другого параметра. Это можно сделать, если для оценки параметра используется шкала отношений. В этом смысле эта шкала является наиболее совершенной, в ней возможны все арифметические действия. Следует отметить, что шкала отноше­ний применима к большинству параметров, представляющих со­бой физические величины: размер, вес, плотность, сила, напря­жение, частота и пр.

Шкала, в которой измеряется тот или иной показатель качества, должна учитываться при оценивании уровня качества продукции.

Шкала наименований — это своего рода качественная, а не количественная шкала, она не содержит нуля и единиц измерений. Примером может служить атлас цветов (шкала цветов). Процесс измерения заключается в визуальном срав­нении окрашенного предмета с образцами цветов (эталонными образцами атласа цветов). Поскольку каждый цвет имеет немало вариантов, такое сравнение под силу опытному эксперту, который обладает не только практическим опытом, но и соответствующими особыми характеристиками зрительных возможностей.

В метрологии шкалой называют также часть отсчетного устройства средства измерений, представляющая собой упорядоченный ряд отметок, со­ответствующих последовательному ряду значений величины, вме­сте со связанной с ними нумерацией. То есть это часть средства из­мерения.

Принцип измерений - это совокупность физических явлений, на которых основаны измерения. Так, измерения массы основаны на использовании силы земного притяжения, измерения линейных размеров - на использовании свойств твердого тела и т.п. Принцип измерения всегда важно знать при разработке процедур поверок.

Под методом измерения понимают прием или совокупность при­емов использования принципов и средств измерений. При прямых измерениях используются следующие основные методы: непосредственной оценки, сравнения с мерой, дифференциальный, нулевой и совпадения. При косвенных измерениях применяют преобразование измеряемой величины в процессе измерений. По условиям измерения методы разделяются на контактный и бесконтактный.

Для большинства рабочих средств измерений применяется метод непосредственной оценки, а для целей метрологических поверок средств измерений - дифференциальный метод

Дата добавления: 2014-01-03