Алгоритм плавающего горизонта

Алгоритм плавающего горизонта чаще всего используется для удаления невидимых линий трехмерного представления функций, описывающих поверхность в виде F(x, y, z) = 0.

Подобные функции возникают во многих приложениях в математике, технике, естественных науках и других дисциплинах.

Предложено много алгоритмов,использующих этот подход. Поскольку в приложениях в основном интересуются описанием поверхности, этот алгоритм обычно работает в пространстве изображения. Главная идея данного метода заключается в сведении трехмерной задачи к двумерной путем пересечения исходной поверхности последовательностью параллельных секущих плоскостей, имеющих постоянные значения координат x, y или z.

На рис. 19.1 приведен пример, где указанные параллельные плоскости определяются постоянными значениями z. Функция F(x, y, z) = 0 сводится к последовательности кривых, лежащих в каждой из этих параллельных плоскостей, например к последовательности y = f(x, z) или x = g(y, z), где z постоянно на каждой из заданных параллельных плоскостей.

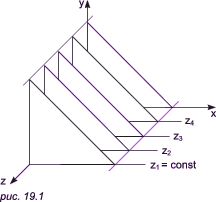
Итак, поверхность теперь складывается из последовательности кривых, лежащих в каждой из этих плоскостей, как показано на рис. 19.2. Здесь предполагается, что полученные кривые являются однозначными функциями независимых переменных.

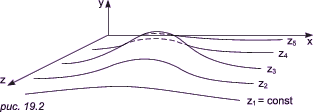
Если спроецировать полученные кривые на плоскость z = 0, как показано на рис. 19.3, то сразу становится ясна идея алгоритма удаления невидимых участков исходной поверхности. Алгоритм сначала упорядочивает плоскости z = const по возрастанию расстояния до них от точки наблюдения. Затем для каждой плоскости, начиная с ближайшей к точке наблюдения, строится кривая, лежащая на ней, то есть для каждого значения координаты x в пространстве изображения определяется соответствующее значение y. Алгоритм удаления невидимой линии заключается в следующем: если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше значения y для всех предыдущих кривых при этом значении x, то текущая кривая видима в этой точке; в противном случае она невидима.

Невидимые участки показаны пунктиром на рис. 19.3. Реализация данного алгоритма достаточно проста. Для хранения максимальных значений y при каждом значении x используется массив, длина которого равна числу различимых точек (разрешению) по оси x в пространстве изображения. Значения, хранящиеся в этом массиве, представляют собой текущие значения «горизонта». Поэтому по мере рисования каждой очередной кривой этот горизонт «всплывает». Фактически этот алгоритм удаления невидимых линий работает каждый раз с одной линией.

Алгоритм работает очень хорошо до тех пор, пока какая-нибудь очередная кривая не окажется ниже самой первой из кривых, как показано на рис. 19.4a. Подобные кривые, естественно, видимы и представляют собой нижнюю сторону исходной поверхности, однако алгоритм будет считать их невидимыми. Нижняя сторона поверхности делается видимой, если модифицировать этот алгоритм, включив в него нижний горизонт, который опускается вниз по ходу работы алгоритма. Это реализуется при помощи второго массива, длина которого равна числу различимых точек по оси x в пространстве изображения. Этот массив содержит наименьшие значения y для каждого значения x. Алгоритм теперь становится таким: если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то текущая кривая видима. В противном случае она невидима. Полученный результат показан на рис. 19.4b.

В изложенном алгоритме предполагается, что значение функции, то есть y, известно для каждого значения x в пространстве изображения. Однако если для каждого значения x нельзя указать (вычислить) соответствующее ему значение y, то невозможно поддерживать массивы верхнего и нижнего плавающих горизонтов. В таком случае используется линейная интерполяция значений y между известными значениями для того, чтобы заполнить массивы верхнего и нижнего плавающих горизонтов, как показано на рис. 19.5.

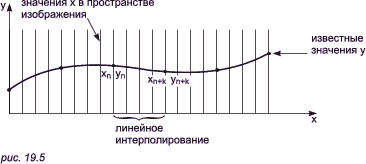
Если видимость кривой меняется, то метод с такой простой интерполяцией не даст корректного результата. Этот эффект проиллюстрирован на рис. 19.6a. Предполагая, что операция по заполнению массивов проводится после проверки видимости, получаем, что при переходе текущей кривой от видимого к невидимому состоянию (сегмент AB на рис. 19.6a), точка (x_n+k, y_n+k) объявляется невидимой. Тогда участок кривой между точками (x_n, y_n) и (x_n+k, y_n+k) не изображается и операция по заполнению массивов не проводится. Образуется зазор между текущей и предыдущей кривыми. Если на участке текущей кривой происходит переход от невидимого состояния к видимому (сегмент CD на рис. 19.6a), то точка (x_m+k, y_m+k) объявляется видимой, а участок кривой между точками (x_m, y_m) и (x_m+k, y_m+k) изображается и операция по заполнению массивов проводится. Поэтому изображается и невидимый кусок сегмента CD. Кроме того, массивы плавающих горизонтов не будут содержать точных значений y. А это может повлечь за собой дополнительные нежелательные эффекты для последующих кривых. Следовательно, необходимо решать задачу о поиске точек пересечения сегментов текущей и предшествующей кривых.

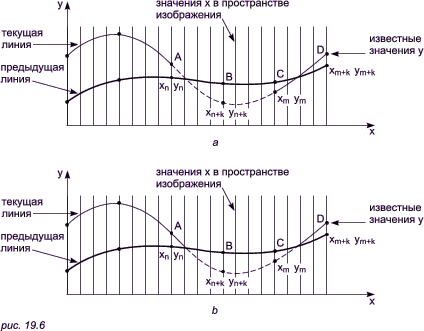
Существует несколько методов получения точек пересечения кривых. На растровых дисплеях значение координаты x можно увеличивать на 1, начиная с x_n или x_m (рис. 19.6a). Значение y, соответствующее текущему значению координаты x в пространстве изображения, получается путем добавления к значению y, соответствующему предыдущему значению координаты x, вертикального приращения Dy вдоль заданной кривой. Затем определяется видимость новой точки с координатами (x + 1, y + Dy). Если эта точка видима, то активируется связанный с ней пиксел. Если невидима, то пиксел не активируется, а x увеличивается на 1. Этот процесс продолжается до тех пор, пока не встретится x_n+k или x_m+k. Пересечения для растровых дисплеев определяются изложенным методом с достаточной точностью. Близкий и даже более элегантный метод определения пересечений основан на двоичном поиске.

Точное значение точки пересечения двух прямолинейных отрезков, которые интерполируют текущую и предшествующую кривые, между точками (x_n, y_n) и (x_n+k, y_n+k) (рис. 19.6) задается формулами:
x = x_n - Dx * (y_np - y_nc)/(Dy_p - Dy_c)
y = m * (x - x_n) + y_n, где
Dx = x_n+k - x_n
Dy_p = (y_n+k)_p - (y_n)_p
Dy_c = (y_n+k)_c - (y_n)_c
m = [(y_n+k) - (y_n)]/Dx,
а индексы c и p соответствуют текущей (current) и предшествующей (previous) кривым. Полученный результат показан на рис. 19.6b.

Теперь алгоритм излагается более формально.

• Если на текущей плоскости при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом х, то текущая кривая видима. В противном случае она невидима.
• Если на участке от предыдущего (x_n) до текущего (x_n+k) значения x видимость кривой изменяется, то вычисляется точка пересечения (x_i).
• Если на участке от x_n до x_n+k сегмент кривой полностью видим, то он изображается целиком; если он стал невидимым, то изображается фрагмент от x_n до x_i если же он стал видимым, то изображается фрагмент от x_i до x_n+k. Заполнить массивы верхнего и нижнего плавающих горизонтов.

Изложенный алгоритм приводит к некоторым дефектам, когда кривая, лежащая в одной из более удаленных от точки наблюдения плоскостей, появляется слева или справа из-под множества кривых, лежащих в плоскостях, которые ближе к указанной точке наблюдения. Этот эффект продемонстрирован на рис. 19.7, где уже обработанные плоскости n - 1 и n расположены ближе к точке наблюдения. На рисунке показано, что получается при обработке плоскости n + 1. После обработки кривых n - 1 и n верхний горизонт для значений x = 0 и 1 равен начальному значению y, для значений x от 2 до 17 он равен ординатам кривой n; а для значений 18, 19, 20 — ординатам кривой n - 1. Нижний горизонт для значений x = 0 и 1 равен начальному значению y, для значений x = 2, 3, 4 — ординатам кривой n; а для значений x от 5 до 20 — ординатам кривой n - 1. При обработке текущей кривой (n + 1) алгоритм объявляет ее видимой при x = 4. Это показано сплошной линией на рис. 19.7. Аналогичный эффект возникает и справа при x = 18. Такой эффект приводит к появлению зазубренных боковых ребер. Проблема с зазубренностью боковых ребер решается включением в массивы верхнего и нижнего горизонтов ординат, соответствующих штриховым линиям на рис. 19.7). Это можно выполнить эффективно, создав ложные боковые ребра. Приведем алгоритм, реализующий эту идею для обеих ребер.

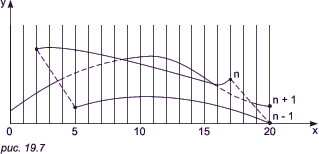
Обработка левого бокового ребра: если P_n является первой точкой на первой кривой, то запомним P_n в качестве P_n-1 и закончим заполнение. В противном случае создадим ребро, соединяющее P_n-1 и P_n. Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним P_n в качестве P_n-1.

Обработка правого бокового ребра: если P_n является последней точкой на первой кривой, то запомним P_n в качестве P_n-1 и закончим заполнение. В противном случае создадим ребро, соединяющее P_n и P_n-1. Занесем в массивы верхнего и нижнего горизонтов ординаты этого ребра и запомним P_n в качестве P_n-1.

Теперь полный алгоритм выглядит следующим образом.

• Для каждой плоскости z = const.
• Обработать левое боковое ребро.
• Для каждой точки, лежащей на кривой из текущей плоскоcти:
• если при некотором заданном значении x соответствующее значение y на кривой больше максимума или меньше минимума по y для всех предыдущих кривых при этом x, то кривая видима (в этой точке). В противном случае она невидима;
• если на сегменте от предыдущего (x_n) до текущего (x_n+k) значения x видимость кривой изменяется, то вычисляется пересечение (x_i);
• если на участке от x_n до x_n+kсегмент кривой полностью видим, то он изображается целиком; если он стал невидимым, то изображается его кусок от x_n до x_i; если же он стал видимым, то изображается его кусок от x_i до x_n+k.
• Заполнить массивы верхнего и нижнего плавающих горизонтов.
• Обработать правое боковое ребро.

Если функция содержит очень острые участки (пики), то приведенный алгоритм может дать некорректные результаты. Этот эффект показан на рис. 19.8.

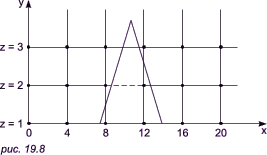
Здесь самая нижняя линия (z = 1) содержит пик. При x = 8 следующая линия (z = 2) объявляется видимой. При x = 12 эта линия (z = 2) объявляется невидимой, определяется точка пересечения и линия (z = 2) изображается от x = 8 до этой точки. На участке от x = 12 до x = 16 эта линия (z = 2) вновь становится видимой, определяется новая точка пересечения и кривая изображается от этого пересечения до x = 16. Следующая линия (z = 3) при x = 8 видима; однако она объявляется видимой и при x = 12. Следовательно, эта линия изображается на участке от x = 8 до x = 12, несмотря на то что она заслонена пиком. Этот эффект вызван вычислением значений функции и оценкой ее видимости на участках, меньших, чем разрешающая способность экрана, то есть тем, что функция задана слишком малым количеством точек. Если встречаются узкие участки, то функцию следует вычислять в большем числе точек. Если в примере на рис. 19.8 функцию вычислять в точках с абсциссами 0, 2, 4,..., 18, 20, вместо точек 0, 4,..., 16, 20, то линия z = 3 будет изображена правильно.

На рис. 19.9 показан типичный результат работы алгоритма плавающего горизонта.

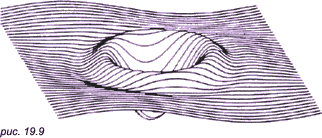
Контрольные вопросы

1. Какие задачи решаются с помощью Алгоритма Брезенхема?

2. В чём состоит первое улучшение алгоритма Брезенхема, второе улучшение алгоритма Брезенхема?

3. В чём заключается алгоритм Флойда-Стейнберга?

4. Что означает термин B-сплайн?

5. С какой целью используют геометрическое сглаживание В-сплайнами?

6. Что означает термин фрактал7

7. Приведите примеры известных фракталов?

8. Перечислите методы удаления невидимых линий. Охарактеризуйте каждый из них.

Дата добавления: 2014-01-03