Лекция №6

Моделирование работы технических объектов на макроуровне

Примеры составления эквивалентных схем технических объектов

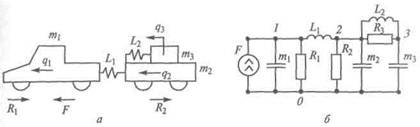
Механические поступательные системы. Рассмотрим пример поступательного движения тягача с нагруженным прицепом. За­кон изменения силы тяги колес тягача известен. Пусть требуется определить скорости поступательного перемещения тягача, при-цепа и груза, а также усилия взаимодействия этих тел. Основными факторами, влияющими на поведение системы, являются инер­ционные свойства тягача, прицепа и груза, упругие свойства сцеп-ки и элементов крепления груза, силы сопротивления перемеще-нию тягача и прицепа с грузом, сила трения груза о платформу прицепа. Допустим, что прочие факторы в расчет не принимают-ся, жесткость учитываемых упругих элементов постоянна, силы сопротивления и трения пропорциональны относительной ско­рости перемещения элементов системы. Структурная схема дина-мической системы тягача с прицепом в этом случае будет иметь вид, представленный на рис. 2.7, а. Здесь т₁ — масса тягача; т₂ — масса прицепа; т_г — масса груза; L₁ — упругость сцепки; L₂ — упругость элементов крепления груза; F — касательная сила тяги колес тягача; R ₁ — сила сопротивления перемещению тягача; R ₂ — сила сопротивления перемещению прицепа с грузом. Внутренняя сила R ₃ трения груза о платформу прицепа на схеме не показана. Система имеет три степени свободы. В качестве обобщенных коор­динат выбираем продольные перемещения тягача q₁ прицепа q₂

и груза q₃.

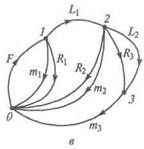
Рис. 2.7. Динамическая система тягача с прицепом:

а — структурная схема; 5 — эквивалентная схема; в — граф

Начало координат связываем с дорогой. На рис. 2.7, б представлена эквивалентная схема объекта, а на рис. 2.7, в — ее граф. Инерционные свойства тягача, прицепа и груза учтены емкостными ветвями, включенными между узлом 0 (дорогой) и узлами 1 (тягач), 2 (прицеп) и 3 (груз). Ветвь F источника силы между узлами 0 и 1 отражает воздействие на тягач внешней силы со стороны дороги. Для учета силы сопротивления движению тя­гача введена ветвь R₁ между узлами 0 и 1, а для учета силы сопро­тивления движению прицепа — ветвь R ₂ между узлами О и 2. Трение груза о платформу прицепа учитывается введением ветви R₃ между узлами 2 u 3. Упругая связь между тягачом и прицепом учтена посредством введения индуктивной ветви L₁ между узлами 1 и 2, а упругость элементов крепления груза — индуктивной ветвью L ₂, включенной между узлами 2 и 3. Потенциал узла 1 характеризует скорость перемещения тягача, узла 2 — скорость перемещения прицепа, узла 3 — скорость перемещения груза относи-тельно дороги. Разность потенциалов в узлах 1 и 2 соответствует скорости перемещения прицепа относительно тягача, в узлах 2 и 3 — скорости перемещения груза относительно прицепа, а в узлах 1 и 3 — скорости перемещения груза относительно тягача. Величины потоков в ветвях схемы соответствуют: для ветви m₁ — силе инерции тягача, ветви т₂ — силе инерции прицепа, ветви т₃ — силе инерции груза, ветви R₁ — силе сопротивления передвижению тягача, ветви R ₂ — силе сопротивления передвижению при­цепа, ветви R ₃ — силе трения груза о платформу прицепа, ветви L₁ — усилию в сцепном устройстве, ветви L ₂ — усилию в элементах крепления груза.

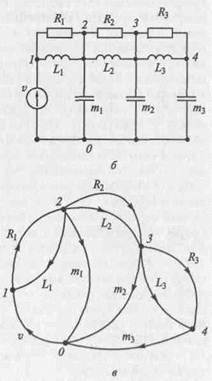
На рис. 2.8 представлены структурная схема трехмассовой динамической системы, эквивалентная схема и ее граф, которые могут быть использованы для исследования вертикальных колебаний остова и сиденья водителя транспортного средства в продольной плоскости. В отличие от примера рис. 2.3 здесь дополни-тельно учтены: радиальная податливость шин L₁ и демпфирование в них R₁, податливость элементов подвески L ₂ и трение в них R ₂, неподрессоренная масса m₁. Масса остова представлена сосредоточенной массой т₂; масса сиденья с водителем — массой m₃; элементы L₃ ^и Rз учитывают упругие и демпфирующие свойства сиденья. Начало координат 0 связано с инерциальной системой, совершающей движение вдоль горизонтальной оси совместно с машиной. Система имеет три степени свободы вдоль вертикальной оси. Обобщенными координатами являются вертикальные перемещения q₁ неподрессоренной массы, центра масс остова q ₂ и сиденья с водителем q₃- Кинематические воздействия на колеса со стороны дороги учтены источником скорости v. Потенциалы в узлах 2, 3 и 4 эквивалентной схемы характеризуют абсолютные вертикальные скорости соответственно неподрессоренных масс, остова и водителя на сиденье. Следует заметить,что эквивалент

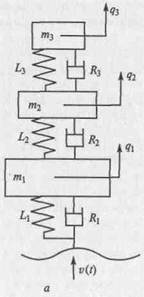
Рис. 2.8. Трехмассовая динами-ческая система:

а — структурная схема; 6 — эквива­ленттай схема; в — граф

ная схема составлена без учета внешних постоянных сил, обусловленных весом остова, неподрессоренных масс и водителя, поэтому математическая модель будет описывать поведение системы относительно ее статического состояния.

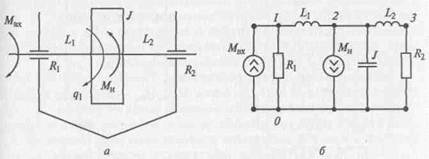
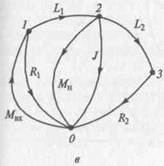
Механические вращательные системы. Рассмотрим фрагмент динамической системы зубчатого редуктора (рис. 2.9, а). Входной вал под действием крутящего момента М_вх вращается на подшип-никах совместно с зубчатым колесом. Потери на трение в под-шипниках учитываются в эквивалентной схеме сопротивлениями R1 и R ₂, крутильные податливости участков валов — элементами L₁ и L ₂, инерционные свойства вала и колеса — элементом J. Влияние остальных элементов редуктора на рассматриваемую подсистему учитывается посредством внешнего момента нагрузки М_н. Эквивалентная схема подсистемы зубчатого редуктора и граф представлены на рис. 2.9, б и в соответственно. Здесь базовый узел 0 соответствует невращающейся части редуктора — корпусу. В качестве обобщенной координаты q₁ выбран угол поворота колеса от­носительно оси вала в направлении действия момента М_вх.

Другим примером механической вращательной системы может служить фрагмент расчетной схемы для исследования динамических процессов, возникающих при включении фрикционного сцепления. Схема динамической системы фрикционного сцепления, его эквивалентная схема и соответствующий ей граф представлены

Рис. 2.9. Динамическая система фрагмента зубчатого редуктора:

о — структурная схема; б — эквивалентная схема; в — граф

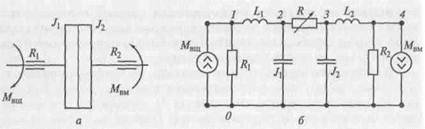
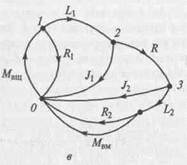
Рис. 2.10. Динамическая система фрикционного сцепления:

а — структурная схема; б — эквивалентная схема; в — граф

на рис. 2.10. Здесь М_вщ, М_вм — соответственно моменты на ведущем и ведомом валах сцепления; J₁ J₂ — вращающиеся массы, учитывающие инерционные свойства соответственно ведущих и ведомых частей; L₁ L₂ — крутильные податливости валов; R₁ R₂ — элементы, учитывающие трение в подшипниках R=R(t) — эле­мент, определяющий закон изменения величины момента трения меҗду дисками в процессе включения сцепления.

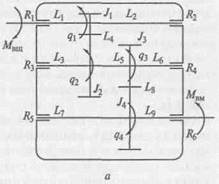
Сложные механические подсистемы. Рассмотрим схему зубчатого редуктора (рис. 2.11, а). Здесь М_вщ, Мвм — крутящие моменты соответственно на ведущем и ведомом валах редуктора; J1- J /₄ — моменты инерции вращающихся масс зубчатых колес и примы-кающих к ним участков валов относительно осей вращения;L1-L3, L5-L7,L9- крутильные податливости участков валов; L₄, L8 — крутильные податливости зубчатых колес первой и второй пары зацепления, приведенные соответственно к угловой скорости промежуточного и выходного валов; R₁ —R₆ — элементы, учитываю­щие трение в подшипниках; q₁ —q₄ — обобщенные координаты (утлы поворота колес).

В этой системе две пары зубчатых колес исполняют роль преобразователей фазовых переменных (крутящего момента и ско­рости), поэтому можно выделить три подсистемы, элементы которых имеют общие фазовые переменные: подсистему ведущего вала, подсистему промежуточного вала и подсистему вы­ходного вала.

Рассмотрим механизм взаимодействия первой пары зубчатых колес. Колесо с моментом инерции J₁ вращаясь с угловой скоро-стью ω₁ = dq₁/dt, имеет контакт с одним концом податливого элемента L₄ колеса с моментом инерции J₂ и сообщает ему (концу податливого элемента) угловую скорость ω₂. Если в данный мо­мент времени ω₂ dq₂/dt, податливый элемент деформируется и в нем возникает упругий момент М_уп. Этот момент воспринимается колесом с моментом инерции J₂ непосредственно, а колесом с моментом инерции J₁ в виде реакции со стороны упругого эле­мента. Обозначим: М' — крутящий момент на первом колесе; М" = М_уп — крутящий момент на втором колесе; D₁ и D ₂ — диа­метры начальных окружностей соответственно первого и второго колес; u₁ — передаточное число первой пары зубчатых колес.

Тогда, пренебрегая потерями в зацеплении, получим

М"/М' =ω1/ω2 =D₂/D₁ =u₁,.

Таким образом, между фазовыми переменными рассматриваемых подсистем существуют однозначные связи, определяемые пе-редаточными числами зубчатых колес, находящихся в зацепле­нии; это позволяет объединить подсистемы и создать математи-ческую модель объекта.

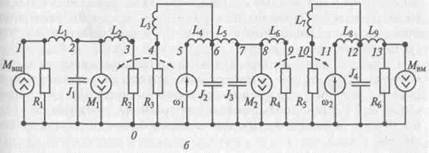
Рис. 2.11. Схема зубчатого редуктора:

а — структурная; б — эквивалентная

На рис. 2.11,6 приведена эквивалентная схема данного редуктора, состоящая из 14 узлов и 25 ветвей. Они являются элементами трех подсистем — по числу валов редуктора. Базовый узел 0связан с корпусом редуктора. Для учета взаимного влияния подсистем ведущего и промежуточного валов используется трансформатор -ная связь: в подсистему ведущего вала между базовым узлом и инерционлым элементом включен зависимый источник момента М1 а в подсистему промежуточного вала зависимый источник угловой скорости ω₁ между базовым узлом и ветвью L₄. Поток в ветви М1 пропорционален потоку в ветви ω₁, а потенциал узла 5 пропорционален потенциалу узла 2. Коэффициенты этих зависимостей определяются передаточным числом u₁ первой пары зубчатых колес. Компонентные уравнения источников момента и ско­рости с учетом выбранного направления обобщенных координат имеют вид

M_0-2=M_0-6/u₁, ω₅=ω₂/u₁

Здесь индексы при переменных соответствуют номерам узлов схемы.

Аналогичная трансформаторная связь с использованием зависимых источников М₂ и ω₂ включена между второй и третьей подсистемами.

В рассмотренном примере упругие свойства первого зубчатого чацепления учитывались крутильной податливостью колес, при-неденной к угловой скорости промежуточного вала, которую можно Пыло бы привести к угловой скорости ведущего вала и учитывать В первой подсистеме. В этом случае индуктивную ветвь следует под-соединить к узлу 2, между ней и базовым узлом поместить зависи­мый источник скорости, а между базовым узлом и инерционным эдементом второй подсистемы (узел 6) — зависимый источник момента.

Рассмотрим пример сложной механической поступательной системы (рис. 2.12), которая представляет собой транспортное сред-ство, движущееся по дороге на пневматических шинах с подрессо-ренным передним мостом и подрессоренным сиденьем водителя. Схема динамической системы транспортного средства представле-иа на рис. 2.12, а. Требуется составить эквивалентную схему объекта Для исследования вертикальных колебаний на сиденье водителя, всртикальных колебаний переднего моста и вертикальных и угловых колебаний остова машины в продольной плоскости. При решеНии задачи в расчет принимаются: инерционные свойства пере­днего моста (масса т₁); инерционные свойства остова (масса т₂ и Момент инерции J); инерционные свойства сиденья с водителем (масса т_ъ); упругие и демпфирующие свойства передних шин (L₁ uR₁); упругие и демпфирующие свойства задних шин (L₂ и R₂); Упругие и демпфирующие свойства передней подвески (L₃и R ₃);

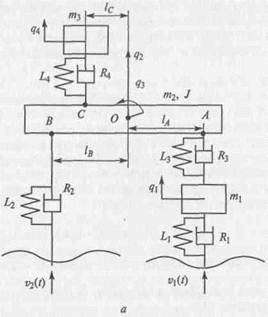
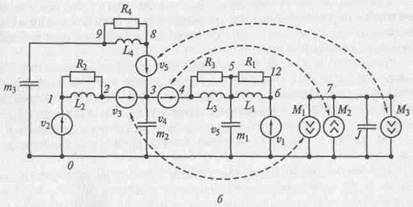
Рис. 2.12. Схема транспортного средства: а — структурная; б — эквивалентная

упругие и демпфирующие свойства сиденья (L₄ и R₄); место расположения элементов конструкция относительно центра масс остова 0 (1_А, 1_В и l_с). Принято, что законы изменения высоты неровностей известны и одинаковы для левого и правого колес.

Основным отличием данного примера от примера рис. 2.8 является то, что здесь учитывается вращение остова в продольной плоскости вокруг его центра масс. Система имеет четыре степени свободы: вертикальные перемещения сосредоточенных масс т1m2, т₃ и поворот массы с моментом инерции Jвокруг оси, проходящей через центр О и перпендикулярной продольной плоскости. В соответствии с этим выбраны обобщенные координаты q1,q2,q3,q4.

Здесь, как и в примере с редуктором (см. рис. 2.11), уравнения контактируемых элементов содержат разные фазовые переменные. Так, точка А (см. рис. 2.12, а) является общей для элементов т₂,J / и L ₃. Но в компонентных уравнениях элемента L₃ фигурируют вертикальная скорость точки А и вертикальная сила (v _А и F _А), для массы остова т₂ уравнения содержат переменные dq ₂/dt и F _А, а в уравнения элемента Jвходят переменные dq₁/dt и момент М_А. Однако меҗду однородными фазовыми переменными этих подсистем существуют однозначные связи:

vА =dq₂/dt + (dq₃/dt) l_a; М_А = F _А1_А.

Аналогичные связи имеют место и в других общих точках системы (В и С):

v_в = dq₂/dt - (dqз/dt)l_B; M_в =-F _в1_в;

vс = dq₂/dt - (dqз/dt)lc; Mc =-Fc 1c;

Наличие таких связей позволяет с помощью дополнительных уравнений, отражающих законы функционирования зависимых источников типа потока и типа потенциала, связать меҗду собой отдельные подсистемы.

На рис. 2.12, приведена эквивалентная схема данного объекта. Здесь базовый узел 0 связан с инерциальной системой, совершающей движение вдоль горизонтальной оси совместно с машиной. Массе т₂ остова, совершающей поступательное движение, соот-ветствует узел 3, вращающейся массе с моментом инерции / — узел 7, массе т_х переднего моста — узел 5, массе т₃ водителя — узел 9.

Для связи подсистем использованы зависимые источники ско-рости Уз, Щ, Щ и зависимые источники момента М_х, М₂, М₃. Вне-шние кинематические возмущения со стороны дороги учтены ис-точниками скорости у_х и р₂. Точке А структурной схемы соответ-ствует узел 4 в эквивалентной схеме, точке В — узел 2, а точке С — узел 8. Влияние вращательной подсистемы на поступатель-ную отражено введением зависимых источников скорости, а вли­яние поступательной на вращательную — введением зависимых источников момента. Чтобы правильно учесть взаимное влияние подсистем, необходимо должным образом задать направления действия источников.

Если вместо расстояний используются продольные коорди­наты общих точек относительно центра масс остова О, направления моментов и скоростей учитывают-ся в компонентных уравнениях зависи-мых источников. На схеме же все зави-симые источники скорости будут направ-лены от узла 3, а все источники момента — к узлу 7.

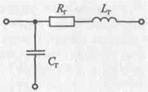
Рис. 2.13. Эквивалентная схема секций трубопро­вода

Гидравлические (пневматические) под-системы. При составлении эквивалентных схем гидравлических и пневматических подсистем за базовый узел обычно при-нимается внешняя среда. Любой трубо-

провод можно представить состоящим из нескольких секций, эк-вивалентная схема каждой из которых имеет вид, представлен-ныйнарис. 2.13.

Пользователь, учитывая конкретные условия, может пренебрегать какими-либо из элементов Rт, С т или Lт. Резервуары, скорость течения жидкости в которых относительно мала и поэтому потери на трение и изменение кинетической энергии потока не-значительны, часто изображаются только емкостными ветвями, подсоединенными одним полюсом к базовому элементу, а вто-рым — к другим элементам трубопровода. Участок трубы относи­тельно болыиой длины и с малым поперечным сечением изобра-жается ветвями гидравлического сопротивления и гидравличес-кой индуктивности, включенными последовательно; изменением объема жидкости пренебрегают.

На рис. 2.14 представлены гидравлическая и эквивалентная схемы гидравлической подсистемы.

Гидравлический насос р качает жидкость, которая по трубопроводу поступает в открытый резервуар С. В эквивалентной схеме насос представлен источником давления р, участок трубопрово­да — индуктивной L и резистивной R ветвями, а резервуар — переменной гидравлической емкостью С.

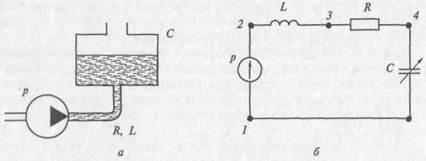
Рис. 2.14. Схема гидравлической подсистемы: а — общая; б — эквивалентная

Разнородные физические подсистемы. В сложных технических системах часто используют элементы, для описания процессов в которых требуются фазовые переменные, характерные для разных физических систем. В подобных случаях целесообразно составлять системы уравнений отдельно для электрической, тепловой и ме-ханической частей (подсистем) сложной системы. Взаимосвязь частей должна проявляться в объединении таких автономно со-ставленных систем уравнений в обшую систему уравнений на опре-деленном этапе моделирования.

В эквивалентных схемах каҗдая подсистема физической систе­мы имеет свое самостоятельное изображение.

Физические элементы, в которых происходит преобразование или иное воздействие переменной одной подсистемы на пере­менные другой, должны иметь описание в более чем одной под-системе. Компонентные уравнения этих элементов должны содер-жать соотношения меҗцу фазовыми переменными двух разнород-ных подсистем.

Ранее было введено понятие внешних параметров как количественных оценок факторов внешней по отношению к подсистеме среды. Предполагалось, что внешние параметры при анализе про­цессов в подсистеме считаются постоянными (например, темпе­ратура) или зависящими только от времени (например, парамет­ры внешней нагрузки). Если же анализу подвергаются процессы взаимодействия подсистем, то очевидно, что многие из внешних параметров уже не могут быть заданы до начала анализа как функции времени. Их текущие значения становятся известными только в процессе совместного решения систем уравнений всех подсис­тем.

Таким образом, взаимовлияние подсистем может быть отраже-но, если внешние параметры одной подсистемы рассматривать как функции фазовых переменных другой подсистемы. При со-ставлении эквивалентных схем это взаимовлияние находит отра-жение либо включением дополнительных ветвей типа источни-ков, либо учетом зависимостей внутренних параметров (сопро-тивлений, емкостей, индуктивностей) уже имеющихся в схеме ветвей от фазовых переменных других подсистем.

Для примера рассмотрим систему с силовым гидравлическим цилиндром, схема которой представлена на рис. 2.15, а. Гидравли-ческий насос качает жидкость в цилиндр и заставляет переме-щаться поршень, нагруженный внешней силой. Давление жидкости на выходе из насоса и закон изменения силы на штоке поршня известны.

Можно выделить две подсистемы: гидравлическую и меха-ническую поступательную. Для каждой из них строится своя эк-вивалентная схема. В эквивалентной схеме гидравлической под­системы насос отображается ветвью внешнего источника дав-

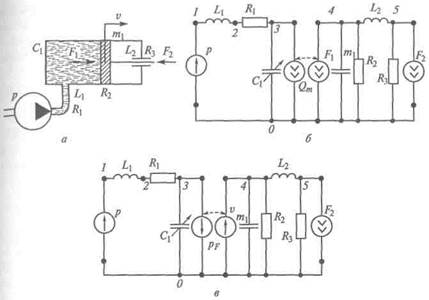
Рис. 2.15. Схема силового гидравлического цилиндра: а — общая; б, в — эквивалентная

ления р, потери в трубопроводе учитываются ветвями L₁ и R, а влияние внутренней полости гидроцилиндра — емкостной ветвью С₁. В схеме механической подсистемы учитываются инерционные свойства поршня (ветвь т₁), трение поршня о стенки цилиндра (ветвь R ₂), трение штока в контакте с уплотнением (ветвь Rз), податливость штока (ветвь L ₂) и внешняя нагрузка (ветвь F ₂).

Взаимодействие подсистем заключается в том, что давление р в цилиндре (узел 3) создает силу F1 действуюшую на поршень. Под ее воздействием поршень перемещается со скоростью v (узел 4), изменяя поток Q _т в цилиндре. На рис. 2.15, бсвязь под­систем учитывается включением в схему зависимых источников типа потока — ветви Q )_т и F₁ компонентные уравнения которых имеют вид

F₁=pS, Qт = pSv,

где S — площадь поршня; р — плотность рабочей жидкости.

Взаимодействие подсистем можно учесть и другим образом. Поток жидкости в полости цилиндра вызывает перемещение пор­шня со скоростью V. При этом давление жидкости в цилиндре зависит от силы, действующей со стороны поршня. Тогда связь между подсистемами может быть учтена включением зависимыхисточников типа потока — ветви p_F и V (рис. 2.15, в), компонентные уравнения которых имеют вид

p=F₁/S, v=Q_m/ρS

В программах анализа, используемых в САПР, автоматизировано как решение, так и формирование ММ объектов. Наиболее общий случай ММ на макроуровне есть ее представление в виде системы ОДУ вида

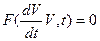
где F — вектор-функция; V — вектор фазовых переменных; t — время.

Данная система состоит из компонентных и топологических уравнений. Обычно пользователь САПР не касается непосредствен-но вопросов, связанных с получением уравнений. Он оперирует эквивалентными схемами, состоящими из набора элементов, соединенных меҗду собой надлежащим образом. Однако использо-вание элементов в схеме предполагает их наличие в библиотеке моделей программного комплекса анализа динамических систем. Первоначально библиотека моделей создается разработчиком САПР и содержит типовой набор моделей, достаточный, по мне-нию разработчика, для решения общих задач анализа ряда техни­ческих систем. По мере использования САПР возникает потреб-ность в расширении набора моделей. В этом случае пользователь обращается к разработчику комплекса или сам пополняет библиотеку.

Задача создания ММ для библиотеки непростая. С ней может справиться только квалифицированный пользователь, обладающий знаниями методов и алгоритмов автоматического получения топологических уравнений. Рядовому пользователю достаточно уметь правильно составить эквивалентную схему, описать ее на входном языке и сформулировать задание на выполнение. После этого ММ объекта будет получена автоматически в соответствии с программой, созданной разработчиком САПР.

В САПР применяются несколько методов формирования ММ объектов, различающихся выбором системы базисных переменных. В основе некоторых из них лежат известные методы, традиционно используемые в различных областях техники, например узловой метод. В теории электрических цепей он известен как метод узловых потенциалов, а в механике — как метод перемещений. В качествеосновного топологаческого уравнения в узловом методе принимают уравнение равновесия, а в качестве базисных координат — фазо-вые переменные, относящиеся к узлам эквивалентной схемы. Уз-ловой метод успешно применяется и для моделирования гидравли-ческих систем. Достаточно известен, но менее распространен в САПР контурный метод; в механике его называют методом сил.

Для эффективного применения некоторых методов численно-го интегрирования ОДУ әти уравнения удобно представлять в нормальной форме Коши:

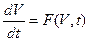
Для получения таких уравнений разработан специальный метод, называемый методом переменных состояния. Иногда применяется табличный метод, который сравнительно прост в реализации, но приводит к созданию модели болыпей размерности. Формальное сходство исходных компонентных и топологических уравнений в системах различной физической природы позволяет применять любой из названных методов для моделирования всей номенкла­туры технических объектов.

Реализация в программе конкретного метода формирования ММ объекта может потребовать от пользователя выполнения допол-нительных правил составления эквивалентных схем. Так, в клас-сическом варианте метода узловых потенциалов имеются ограни-чения на вид компонентных уравнений. Применительно к схем-ной форме представления моделей әти ограничения выражаются в недопустимости таких ветвей, как идеальные источники типа потенциал а, и любых ветвей, параметры которых зависят от ка-ких-либо потоков. Использование метода переменных состояния подразумевает отсутствие в эквивалентной схеме контуров, со-стоящих только из емкостных ветвей (возможно, с источниками типа потенциала), и узлов, в которых объединяются только индуктивные ветви или только резистивные ветви (возможно, с ис­точниками типа потока). Подобные ограничения можно снять ис-пользованием фиктивных ветвей.

Каждый метод имеет свои особенности, касающиеся формы описания исходных данных, но синтаксис входного языка описа-ния объекта в большей мере определяется все же разработчиком программного комплекса, который и создает этот язык.

Итак, чтобы иметь возможность использовать в своей работе процедуры математического моделирования работы технических объектов на макроуровне пользователю САПР необходимо:

уметь составлять эквивалентные схемы объектов;

иметь программный комплекс для анализа систем;

изучить особенности комплекса в части составления эквива­лентных схем и язык комплекса.

Для выполнения моделирования пользователю достаточно:

разработать эквивалентную схему объекта с учетом особеннос-тей программного комплекса и возможностей его библиотеки ММ элементов;

активизировать программу анализа;

с помощью входного языка комплекса описать структуру объекта и параметры элементов схемы;

с помощью входного языка описать задание на выполнение моделирования;

обработать полученные результаты.

Дата добавления: 2014-01-03