Вычисление факториала

Begin

write('Ведите натуральное число в 10-сс: ');

readln(x);

writeln('Переведем ', x,' в 2-сс: ');

a:=x; {сохраняем исходное число в дополнительной переменной а}

write('1 способ - с помощью итерации (цифры в обратном порядке): ');

{цифры двоичного представления вычисляются в обратном порядке (сначала последние)}

while x>0 do

begin

c:=x mod 2;

x:=x div 2;

write(c);

end;

writeln;

write('2 способ - с помощью рекурсии: ');

BinaryRepresentation(a);

readkey;

end.

Классическим примером рекурсивной функции является вычисление факториала. Из курса математики известно, что 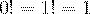, 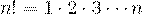. С другой стороны .

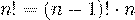Таким образом, нам известны два частных случая параметра 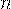, а именно и , при которых мы без каких-либо дополнительных вычислений можем определить значение факториала.

Во всех остальных случаях, то есть для 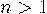, значение факториала может быть вычислено через значение факториала для параметра .

Таким образом, рекурсивная подпрограмма будет иметь вид:

function Factorial (n:byte):longint;
begin

if (n=0) or (n=1) {описываются условия граничных случаев}

then Factorial:=1 {точка возврата или остановка рекурсии}
else Factorial:= Factorial (n-1)*n; { шаг рекурсии }

end;

Или так

function Factorial (n:byte):longint;
begin

if n>0 then Factorial:= Factorial (n-1)*n; { шаг рекурсии }

else Factorial:=1 {точка возврата или остановка рекурсии}
end;

На рисунке 16.2 показан процесс вычисления для случая Factorial(4).

Первый вызов функции осуществляется из основной программы, например a:= Factorial(4). Он продолжается до тех пор, пока значение локальной переменной не становится равной 1. После этого начинается выход из рекурсии. В результате вычислений получается, что Factorial(4)=4*3*2*1.

Сначала образуется так называемый рекурсивный фрейм №1 при n=4. Для этого фрейма отводится память и в нем фиксируются все значения переменных тела функции при n=4. Отметим, что в рекурсивном фрейме фиксируются значения всех переменных функции, кроме глобальных.

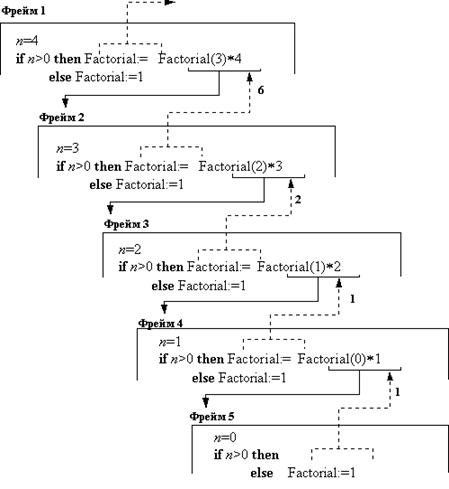
Рис. 16.2. Вычисление функции Factorial(n) для n=4.

Затем происходит вызов Factorial(n) при n=3. Образуется фрейм №2, где фиксируются значения переменных тела функции при n=3. При этом фрейм №1 также хранится в памяти. Из фрейма №2 происходит обращение к Factorial(n) при n=2. В результате этого обращения образуется фрейм №3, где фиксируются значения переменных тела функции при n=2 и т.д. до тех пор, пока при очередном обращении к функции Factorial условие n>0 не примет значение false.

Это произойдет в фрейме №5. В этом фрейме мы получим значение Factorial =1 и передадим это значение в фрейм №4. После этого фрейм №5 будет уничтожен, так как обращение Factorial(n) при n=0 будет выполнено.

В фрейме №4 мы вычислим значение Factorial(n) для n=1. После чего мы передадим это значение во фрейм №3, а фрейм №4 будет закрыт, так как обращение к Factorial(n) при n=1 будет закончено.

Так мы будем сворачивать эту цепочку фреймов в последовательности, обратной той, в которой мы их порождали, пока не свернем фрейм №1. После чего вычисление функции будет окончено.

Рекурсивные подпрограммы применяют для компактной записи алгоритмов, имеющих рекурсивную природу.

Любую рекурсивную подпрограмму можно реализовать без применения рекурсии. Запись ее в этом случае может значительно удлиниться, зато уменьшится расход времени и памяти на повторные вызовы и передачи копий параметров.

Существует два важных положения, известных в математике и в программировании, определяющих соотношение между итерацией и рекурсией:

Дата добавления: 2014-01-03