
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Микроалгоритм выравнивания порядков чисел и его схемная реализация
|
|
|
|
Выравнивание порядков осуществляется путем сдвига вправо мантиссы числа, порядок которого меньше. Так как сдвиг вправо эквивалентен делению мантиссы на k, то при каждом сдвиге порядок должен увеличиваться на 1. Например, если 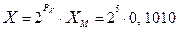 , а
, а 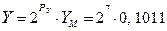 , то мантиссу числа X необходимо сдвинуть вправо на 2 разряда, т.е.
, то мантиссу числа X необходимо сдвинуть вправо на 2 разряда, т.е. 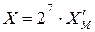 , где
, где 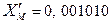 . Для выравнивания порядков необходимо прежде всего определить, порядок какого числа меньше. Это можно осуществить с помощью специальной схемы сравнения слов. Но так как при выполнении умножения и деления порядки чисел складываются и вычитаются, то в АЛУ всегда имеется сумматор порядков. Поэтому для определения числа с меньшим порядком используется сумматор порядков. Для этого из порядка первого числа вычитается порядок второго числа. По знаку разности определяется больший порядок, а абсолютная величина разности позволяет определить необходимое число сдвигов. Так как над порядками производятся только операции сложения или вычитания, то для их представления удобно использовать дополнительные коды. Таким образом, МА выравнивания порядков чисел X и Y сводится к следующему:
. Для выравнивания порядков необходимо прежде всего определить, порядок какого числа меньше. Это можно осуществить с помощью специальной схемы сравнения слов. Но так как при выполнении умножения и деления порядки чисел складываются и вычитаются, то в АЛУ всегда имеется сумматор порядков. Поэтому для определения числа с меньшим порядком используется сумматор порядков. Для этого из порядка первого числа вычитается порядок второго числа. По знаку разности определяется больший порядок, а абсолютная величина разности позволяет определить необходимое число сдвигов. Так как над порядками производятся только операции сложения или вычитания, то для их представления удобно использовать дополнительные коды. Таким образом, МА выравнивания порядков чисел X и Y сводится к следующему:
(BG)
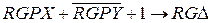 (такт 1)
(такт 1)

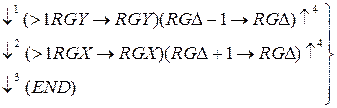 (такт 2)
(такт 2)
Например, при 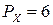 и
и 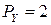 получим:
получим:
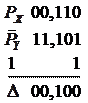
Так как 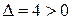 , то для выравнивания порядков необходимо мантиссу Y сдвинуть на 4 разряда вправо. Схема, реализующая описанный МА, показана на рис. 6.1. Порядки
, то для выравнивания порядков необходимо мантиссу Y сдвинуть на 4 разряда вправо. Схема, реализующая описанный МА, показана на рис. 6.1. Порядки 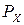 и
и 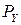 поступают на SM и по сигналу ST фиксируются в виде разности
поступают на SM и по сигналу ST фиксируются в виде разности 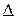 на
на 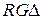 с дешифрированным нулевым состоянием (= 0). Знак SI разности
с дешифрированным нулевым состоянием (= 0). Знак SI разности 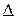 анализируется и каждый тактовый сигнал C при наличии разрешения с триггера T1 формирует сигнал МО (рис. 6.2) правого сдвига мантиссы на RGX (> RGX) или RGY (> RGY) и МО
анализируется и каждый тактовый сигнал C при наличии разрешения с триггера T1 формирует сигнал МО (рис. 6.2) правого сдвига мантиссы на RGX (> RGX) или RGY (> RGY) и МО 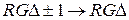 . Операция завершается по сигналу (= 0) на
. Операция завершается по сигналу (= 0) на 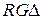 . Триггер T2 служит для запоминания того числа, порядок которого больше. После выравнивания порядков осуществляется суммирование мантисс, которое ничем не отличается от способов суммирования чисел с фиксированной запятой. Результату присваивается порядок большего по абсолютной величине операнда, т. е. того, мантисса которого оставалась неподвижной при выравнивании порядков. Установить этот факт можно с помощью триггера T2 на рис. 6.1.
. Триггер T2 служит для запоминания того числа, порядок которого больше. После выравнивания порядков осуществляется суммирование мантисс, которое ничем не отличается от способов суммирования чисел с фиксированной запятой. Результату присваивается порядок большего по абсолютной величине операнда, т. е. того, мантисса которого оставалась неподвижной при выравнивании порядков. Установить этот факт можно с помощью триггера T2 на рис. 6.1.
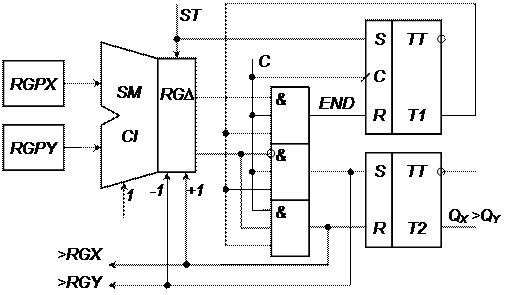 |
Рис. 6.1. Схема выравнивания порядков
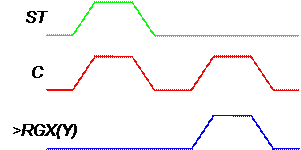 |
Рис. 6.2. Временная диаграмма работы схемы выравнивания порядков
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1695; Нарушение авторских прав?; Мы поможем в написании вашей работы!