Разряды числа

1. Числа второго десятка (двадцаток).
2. Числа первой сотни.
3. Числа первой тысячи.
4. Многозначные числа.
5. Системы счисления.

1. Числа второго десятка (двадцаток)

Числа второго десятка (11,12,13,14,15,16,17,18,19,20) – двузначные числа.

Для записи двузначного числа используются две цифры. Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа - цифра второго разряда или разряда десятков.

Числа второго разряда во всех учебниках математики для начальных классов рассматриваются отдельно от других двузначных чисел. Это объясняется тем, что названия чисел второго десятка противоречат способу их записи. Поэтому многие дети некоторое время путают порядок записи цифр в числах второго десятка, хотя называть их при этом могут правильно.

Например, при записи на слух числа 12 (две-на-дцать) ребенок первым словом слышит «две(а)», поэтому он может записать цифры в таком порядке 21, но прочитать эту запись как «двенадцать».

Формирование представления о двузначных числах строится на основе понятия «разряд».

Понятие разряда является базовым в десятичной системе счисления. Под разрядом понимается определенное место в записи числа в позиционной системе счисления (разряд – это позиция цифры в записи числа).

Каждая позиция в этой системе имеет свое название и свое условное значение: цифра, стоящая на первой позиции справа, означает количество единиц в числе: цифра, стоящая на второй позиции справа, означает количество десятков в числе и т.д.

Цифры от 1 до 9 называют значащими, а нуль является незначащей цифрой. При этом его роль в записи двузначных и других многозначных чисел очень важна: нуль в записи двузначного (и т.д.) числа означает, что число содержит обозначенный нулем разряд, но значащих цифр в нем нет, т.е. наличие нуля справа в числе 20, обозначает, что цифра2 должна восприниматься как символ десятков, и при этом число содержит только два целых десятка; запись 23 будет означать, что кроме 2 целых десятков число содержит еще 3 единицы, дополнительно к целым десяткам.

Понятие «разряд» играет большую роль в системе изучения нумерации, а также является основой для освоения так называемых «нумерационных» случаев сложения и вычитания, в которых действия производятся целыми разрядами:

27 – 20 365 – 300

27 - 7 365 - 60

20 + 7 305 + 60

Умение узнавать и выделять в числах разряды является основой умения раскладывать числа на разрядные слагаемые: 34 = 30 + 4

Для числа второго десятка понятие «разрядный состав» совпадает с понятием «десятичный состав». Для двузначных чисел, содержащих более одного десятка – эти понятия не совпадают. Для числа 34 десятичный состав – это 3 десятка и 4 единицы. Для числа 340 разрядный состав – это 300 и 40, а десятичный – это 34 десятка.

Знакомство с числами второго десятка (11-20) удобно начинать со способа их образования и названия чисел, сопровождая его сначала моделью на палочках, а затем чтением числа по модели:

один-на-дцать три-на-дцать сем-на-дцать

Запоминание названий двузначных чисел в этом случае не будет затруднено для детей противоречащей названию записью: 11,13,17. (Ведь в соответствии с традицией чтения в европейских письменностях слева направо в названии этих чисел сначала должна была ба идти цифра десятков, а потом цифры единиц!). В связи с такой особенностью чисел второго десятка, многие дети в первом классе долго путаются при записи их на слух и чтении по записи. Раннее введение символики играет в данном случае отрицательную роль как для запоминания названий чисел второго десятка, так и для понимания их структуры. Для формирования правильного представления о структуре двузначного числа следует всегда класть десятки слева, а единицы справа. Таким образом ребенок зафиксирует во внутреннем плане правильный образ понятия, без специальных многословных и не всегда понятных ему объяснений.

На следующем этапе предлагаем ребенку соотнесение вещественной модели и символической записи:

13 15 17

Затем переходим на графические модели и к чтению чисел по графической модели:

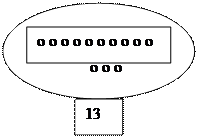
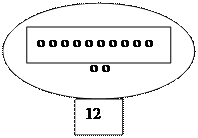
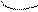о о

о о о

о о о о

о о о о о

о

оо о

Далее вводятся схематические разрядные модели:

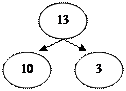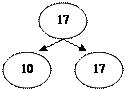А затем символическая запись разрядного состава чисел второго десятка: 17 = 10+7.

В дальнейшем в школе вводят понятие разряда и знакомят детей с понятием «разрядные слагаемые»:

37 = 30 + 7; 624 = 600 + 20 + 4.

Использование десятичной модели вместо разрядной для знакомства со всеми двузначными числами позволяет без введения понятия «разряд» познакомить ребенка как со способом образования этих чисел, так и научить его читать число по модели (и наоборот, строить модель по названию числа), а затем и записывать:

32 45

При изучении детьми чисел второго порядка рекомендуем педагогу использовать следующие виды заданий:

1) на способ образования чисел второго десятка:

Покажи тринадцать палочек. Сколько это десятков и сколько еще отдельных палочек?

2) на принцип образования натурального ряда чисел:

Сделай рисунок к задаче и реши ее устно. «В городе было 10 кинотеатров. Построили еще 1. Сколько кинотеатров стало в городе?»

Уменьши на 1: 16,11,13,20

Увеличь на 1: 19,18,14,17

Найди значение выражения: 10+1; 14+1; 18-1; 20-1.

(Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на 1 – к получению числа предыдущего.)

3) на поместное значение цифры в записи числа:

Что обозначает каждая цифра в записи числа: 15, 13, 18, 11, 10, 20?

(В записи числа 15 цифра 1 обозначает количество десятков, а цифра 5 – количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет.)

4) на место числа в ряду чисел:

Вставь пропущенные числа: 12… … … 16 17 … 19 20

Вставь пропущенные числа: 20… 18 17 … … … 13 … 11

(При выполнении задания ссылаются на порядок чисел при счете)

5) на разрядный (десятичный) состав:

10 + 3 = … 13 – 3 = … 13 – 10 = …

12 = 10 + … 15 = … + 5

При выполнении задания ссылаются на разрядную (десятичную) модель числа из десятка (пучка палочек) и единиц (отдельных палочек.

6) на сравнение чисел второго десятка:

Какое из чисел больше: 13 или 15? 14 или 17? 18 или 14? 20 или 12?

При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при свете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 13 две единицы получим 15, значит 15 больше, чем 13).

Сравнивая числа второго десятка с однозначными числами, следует ссылаться на то, что вес однозначные числа меньше, чем двузначные:

Назови самое большое и самое маленькое из этих чисел: 12 6 18 10 7 20.

При сравнении чисел второго десятка удобно пользоваться линейкой.

0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26

Сравнивая длины соответствующих отрезков, ребенок наглядно определяет постановку знака сравнения: 17<19.

1. Числа первой сотни

Десять десятков – это сотня. Числа от 11 до 100 называют числами первой сотни. Все числа первой сотни – двузначные.

Двузначные числа записывают двумя цифрами: 37, 45, 64, 40.

Первая цифра справа в записи двузначного числа называется цифрой первого разряда или разряда единиц, вторая цифра справа – цифрой второго разряда или разряда десятков.

Целые десятки (10 20 30 40 50 60 70 80 90) иногда именуются разрядными числами.

Читают двузначные числа слева направо. Для чисел 21 – 100 порядок называния составляющих их разрядных чисел и порядок записи совпадает: 21 (два – дцать один).

Понятие «разряд» является базовым для образования чисел первой сотни.

Разрядный состав - выделение разрядных чисел в двузначном числе:

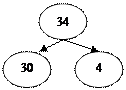На основе разрядного состава рассматриваются случаи разрядного сложения и вычитания:

30 + 4 34 – 4 34 – 30

При нахождении значений этих выражений ссылаются на разрядный состав двузначных чисел: число 34 состоит из 30 и 4. Вычитая 30 получаем 4.

Разрядные слагаемые – сумма разрядных чисел двузначного числа:

47 = 40 + 7 68 = 60 + 8

Десятичный состав – выделение десятков и единиц в двузначном числе:

26 – это 2 дес. и 6 ед.

Схема десятичного состава

На основе схемы десятичного состава можно рассмотреть такие случаи сложения и вычитания:

26 – 6 26 – 20 26 – 10 26 – 16 20 + 6

При нахождении значения этих выражений ссылаются на десятичный состав (десятичную схему) двузначного числа: вычитая из числа 26 число 16 (1 десяток и 6 единиц) получаем 1 десяток. Для наглядности ребенок прикрывает вычитаемое рукой на схеме. В дальнейшем это действие ребенок выполняет мысленно и сразу называет и пишет ответ. Использование десятичной схемы двузначного числа значительно облегчает вычислительную деятельность детям, которым вычисления «в уме» даются трудно. Например, десятичная схема числа 57 дает возможность без применения каких – либо еще вспомогательных приемов вычислений решать следующие примеры:

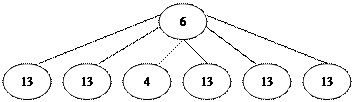57 – 10 57 – 20 57 – 30

57 – 40 57 – 50 50 + 7

57 – 17 57 – 27 57 – 37

57 – 47

а также легко справиться со случаями вида: 57 + 2; 57 + 3; 57 + 10 и т.п., используя прием «десятки к десяткам, а единицы к единицам».

При изучении нумерации двузначных чисел рассматриваются также случаи сложения и вычитания, базирующиеся на принципе построения последовательности натуральных чисел: 43 + 1; 43 – 1; 40 + 1; 40 – 1.

При нахождении значения этих выражений, ссылаются на принцип построения натурального ряда чисел: прибавляя к числу 1, получаем число следующее (последующее). Вычитая из числа 1, получаем число предыдущее.

Приведем основные виды заданий, выполняемых детьми при изучении чисел первой сотни:

1) на способ образования чисел первой сотни:

Назови число, в котором 1дес. 9ед., 2дес. 7ед., 9дес. 2ед.

Запиши числа, в которых 3дес. 7ед.,7дес. 3ед., 7дес. 0ед.

2) на соотнесение количественной модели, названия и записи числа:

Сколько кубиков в каждом рисунке?

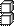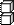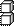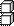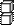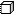
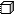
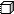
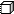
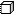
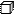
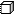
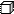
Прочитай и запиши число по модели:

Десятки

Единицы

 

 

3) на принцип образования натурального ряда чисел:

Уменьши на 1: 20, 47, 32, 50, 70

Увеличь на 1: 19, 28, 44, 67, 40, 90

Найди значение выражения: 50+1; 44+1; 68-1; 90-1.

Во всех случаях можно ссылаться на то, что добавление 1 ведет к получению числа последующего, а уменьшение на1 – к получению числа предыдущего.

4) На поместное значение цифры в записи числа:

Что обозначает каждая цифра в записи числа: 72, 20, 70, 27?

(В записи числа 72 цифра 7 обозначает количество десятков, а цифра 2 – количество единиц. В записи числа 20 цифра 2 обозначает, что в числе 2 десятка, а цифра 0 обозначает, что в первом разряде единиц нет).

5) на место числа в ряду чисел:

Вставь пропущенные числа: 40, 41 … 43 … … … 47 … … 50

Вставь пропущенные числа: 70, 69 … … … … 64 … … 61 …

При выполнении задания ссылаются на порядок чисел при счете.

6) на разрядный состав:

20 + 3 = 23 23 – 3 = … 23 – 20 = …

37 = 30 + 7 37 – 30 = … 37 – 7 = …

При выполнении задания ссылаются на разрядную модель числа из десятков и единиц.

7) на сравнение чисел первой сотни:

Какое из числе больше:23или32? 44или47? 28или54? 20или4?

При выполнении задания можно сравнивать две модели чисел из палочек (количественная модель), или ссылаться на порядок следования чисел при счете (меньшее число называют при счете раньше), или опираться на процесс присчитывания и отсчитывания (присчитывая к 44 три единицы получим 47, значит 47 больше, чем 44).

Более соответствующим данному этапу изучения нумерации считается способ сравнения чисел с опорой на разрядный состав. При этом сравнивать числа начинают со старших разрядов: в числе 23 – два десятка, а в числе 32 – три десятка, значит 32 > 23. Если количество десятков одинаковое, то сравнивают цифры разряда единиц: в числе 44 и числе 47 по 4 десятка, сравним разряд единиц – 7 больше, чем 4, значит 47>44.

Сравнивая двузначные числа с однозначными числами, следует ссылаться на то, что все однозначные числа меньше, чем двузначные.

При сравнении чисел вида:

99 … 100 67 … 68

98 … 99 59 … 60

100 … 100 20 … 21

следует ссылаться на порядок следования чисел при счете: следующее число всегда больше, чем предыдущее.

Для наглядного сравнения чисел первой сотни можно использовать портновскую ленту.

8) на десятичный состав двузначных чисел:

Сколько десятков в числе 56, 78, 92?

Комплексное задание на нумерацию двузначных чисел включает полную характеристику заданного числа.

Что можно рассказать о числе 33? (57, 62)

(Это число двузначное, записано с помощью двух цифр. В этом числе 3 десятка и 3 единицы II разряда и 3 единицы I разряда; при счете его называют после числа 32 и перед числом 34 (или – его соседи 32 и 34); оно больше, чем число 30 и меньше, чем число 40; его можно представить в виде суммы 30 и 3)

Завершает изучение чисел первой сотни знакомство с числом 100.

Десять десятков – это сотня.

Число 100 завершает изучение чисел первой сотни

Сотня (100) – первое трехзначное число в ряду натуральных чисел.

Сотня – наименьшее трехзначное число.

Сотня – новая счетная единица в десятичной системе счисления.

В записи числа 100 цифра 1 обозначает, что в III разряде (разряде сотен) – одна единица, а разряд десятков и единиц нули означают, что в этих разрядах нет значащих цифр.

Дата добавления: 2014-01-03