Дифференцирующие и интегрирующие цепи

Проанализированные выше RL – и RС – цепи широко используются в вычислительной и импульсной технике в качестве цепей, позволяющих получать таки и напряжения, пропорциональные производным и интегралам от входного напряжения, а также для преобразования формы входных импульсов.

Дифференцирующие цепи имеют вид, соответствующий рис. (2.29,а) интегрирующие цепи соответствуют рис. (2.29,б).

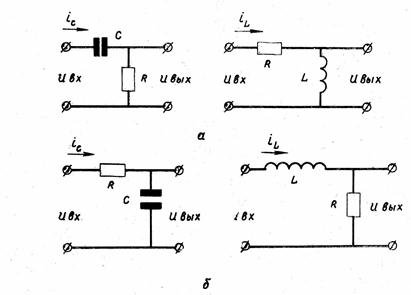
Рис. 2.29

Для цепей рис. 2.29,а справедливы соотношения:

для цепи RС: u _вх = u _С + u _выхC

для цепи RL: u _вх = u _R + u _выхL

Но:

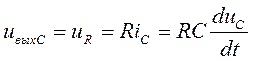, (2.64)

а u _C = u _вх – u _выхC. (2.64,а)

Соответственно:

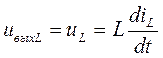, (2.65)

а u _R = u _вх – u _выхL = i_L R, поэтому 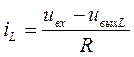(2.65,а)

Подставив (2.64,а) в (2.64), а (2.65,а) в (2.65), получим:

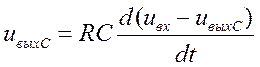
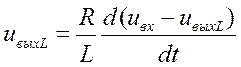
Таким образом, очевидно, что для обеих цепей выходное напряжение может быть записано в общем виде

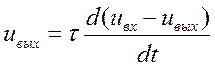(2.66)

где τ — постоянная времени цепи.

Из выражения (2.66) следует, что дифференцирование входного напряжения u _вх тем точнее, чем меньше u _вых по сравнению с u _вх, т. е. при u _вх >> u _вых. Анализ показывает, что это неравенство выполняется, когда постоянная времени τ значительно меньше длительности входного сигнал u _вх или его дифференцируемой части.

Для цепей, изображённых на рис 2.29,б справедливы следующие соотношения:

для цепи RС: u _вх = u _R + u _выхC

для цепи RL u _вх = u _L + u _выхL

Но для цепи RС:

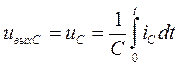, (2.67)

где 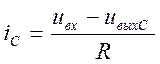, (2.67,а)

поэтому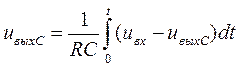

Аналогично для цепи RL

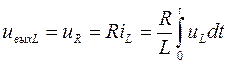, (2.68)

где u _L = u _вх – u _выхL (2.68,а)

Подставив (2.28,а) в (2.68), получим:

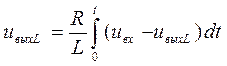
Очевидно, что также, как и в случае дифференцирования, для обеих цепей выходное напряжение может быть записано в общем виде

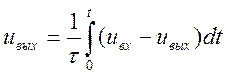, (2.69)

откуда следует, что интегрирование входного напряжения u_вх тем точнее, чем меньше u_вых по сравнению с u _вх, как и в случае дифференцирующих цепей. Анализ показывает, что для интегрирующих цепей это условие выполняется, когда постоянная времени τ значительно больше длительности входного сигнала или его интегрируемой части.

Для u_вх, представляющего собой идеальный прямоугольный импульс, выходное напряжение дифференцирующих цепей имеет вид двух коротких импульсов, соответствующих фронту и срезу импульса (см. рис. 2.30,а), выходное напряжение интегрирующих цепей имеет форму треугольных импульсов, нарастающая и спадающая части которых приблизительно линейны (см. рис. 2.30,б).

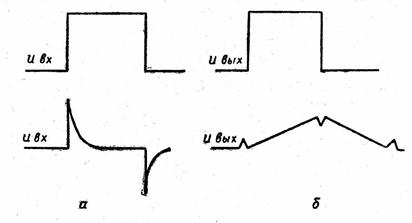
Рис.2.30

Получаемая форма выходного напряжения дифференцирующих и интегрирующих цепей легко объясняется с помощью соотношений, приведенных выше при анализе переходных процессов в RL – и RC – цепях. Реальная, экспериментально полученная, форма выходных импульсов интегрирующих RL – цепей искажается в результате влияния собственной паразитной емкости катушек индуктивности, как показано на рис.2.30,б. Отмеченное влияние паразитной ёмкости ограничивает применение интегрирующих и дифференцирующих RL – цепей по сравнению с RC – цепями.

Дата добавления: 2014-01-03