
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Изображение обобщенных объектов
|
|
|
|
Сложные объекты
Обобщенный объект представляет собой объект, в котором явным образом выделены подклассы. Разбиение класса на подклассы осуществляется по какому-то признаку (свойству).
Свойство, по которому производится разбиение класса на подклассы, называется дискриминатором. Например, подклассы «ВОЕННООБЯЗАННЫЕ» и «НЕВОЕННООБЯЗАННЫЕ» выделяются в зависимости от значения свойства «отношение к воинской обязанности»; подклассы «СТУДЕНТЫ», «АСПИРАНТЫ», «ДОКТОРАНТЫ», «ДОВУЗ» выделяются в зависимости от значения свойства «вид обучения».
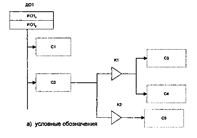
Для обозначения подкласса в схеме будем использовать треугольник, который связан с обозначением свойства, по которому производится разбиение на подклассы, и к которому присоединены обозначения свойств, присущих данному подклассу. Широкая часть треугольника направлена в сторону «родового» объекта, острый угол - в сторону «видового» (рис. 22а).
Рис. 22. Изображение обобщенного объекта
| 
|
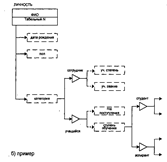
На рис. 22. б) изображен фрагмент инфологической модели, отражающий обобщенный объект «ЛИЧНОСТЬ» для высшего учебного заведения. Для него выделено несколько категорий объектов: «ПРЕПОДАВАТЕЛЬ», «СТУДЕНТ», «АСПИРАНТ». Естественно, что классификация может быть многоуровневой. Так, в рассматриваемомпримере обобщенный объект «ЛИЧНОСТЬ» может быть разбит на два подкласса:«СОТРУДНИК» и «УЧАЩИЙСЯ». «СОТРУДНИКИ», в свою очередь, могут быть классифицированы на «П1ЮФЕССОРСКО-ПРЕПОДАВАТЕЛЬСКИИ СОСТАВ», «АДМИ» и т.д.
Кроме того, подклассы в совокупности могут составлять исходный класс (полный класс), а могут представлять лишь часть ее (неполный класс). Если при описании предметной области возникает необходимость отобразить эту информацию, то для полного класса будем изображать двойную линию, перечеркивающую линию, идущую от дискриминатора; если класс неполный, то будем изображать одинарную линию, перечеркивающую линию, идущую от дискриминатора. Подкласс, как и класс, является совокупностью однотипных объектов. Отображать ту или иную сущность в виде отдельного класса или подкласса в составе обобщенного объекта зависит от проектировщика. Изображение в виде обобщенного объекта является более информативным и, как следствие, дает больший выбор при принятии решений на стадии построения даталогической модели. При использовании обобщенного объекта связи между объектами могут идти как к знаку всего обобщенного объекта, если объекты всех подклассов участвуют в данной связи, так и к знаку отдельного подкласса, если связь относится только к данному подклассу.
Обобщенный объект следует вводить в модель в том случае, когда надо подчеркнуть общность и различие категорий объектов, входящих в один класс, или в случае, если объекты разных подклассов участвуют в разных связях,
Информация о пересекающихся классах
Выделенные в предметной области классы объектов могут быть как пересекающимися, так и непересекающимися1. Для отображения этих сведений в инфологической модели можно использовать граф пересечений, вершины которого соответствуют классам (подклассам) объектов, а ребра связывают пару вершин лишь в том случае, если соответствующие классы объектов являются пересекающимися.
Для отображения степени пересечения можно воспользоваться взвешенным графом. При этом вес вершины будет обозначать мощность соответствующего множества объектов, а вес ребра - мощность множества, являющегося пересечением множеств, связанных этим ребром.
Рис. 23 Фрагмент графа пересечений
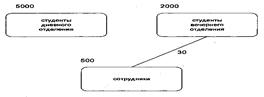
Эту же информацию можно отразить и в табличной форме (табл. 2.3)
Таблица 2.3
| КЛАСС 1 | КЛАСС 2 | Объект пересечения |
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 536; Нарушение авторских прав?; Мы поможем в написании вашей работы!