
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Графическое изображение вариационного ряда
|
|
|
|
Графическое изображение вариационных рядов облегчает их анализ и позволяет судить о форме распределения. Для графического изображения вариационного ряда в статистике строят гистограмму, полигон и кумуляту распределения.
Гистограмма - столбиковая диаграмма, для построения которой на оси абсцисс откладывают отрезки, равные величине интервалов вариационного ряда. На отрезках строят прямоугольники, высота которых в принятом масштабе по оси ординат соответствует частотам (или частостям) (рис. 1).
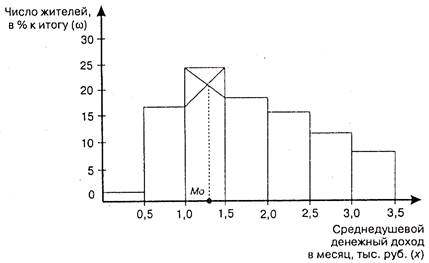
Рис.1.Гистограмма распределения населения по величине среднедушевого дохода
Для графического изображения дискретного вариационного ряда применяют полигон распределения, для построения которого необходимо соединить прямыми отрезками точки с координатами х, ω (рис. 2). Крайние точки полученного графика соединяют с точками по оси абсцисс, отстающими на одно деление в принятом масштабе от минимального и максимального значения вариант. Полигон может быть построен и для интервального вариационного ряда, для этого в качестве координат по оси абсцисс используют середины интервалов. Очевидно, что гистограмма легко может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединить отрезками прямых, при этом середины верхних сторон двух крайних прямоугольников соединить с осью абсцисс в точках, отстоящих в принятом масштабе на величину интервалов от середины первого и последнего интервалов.
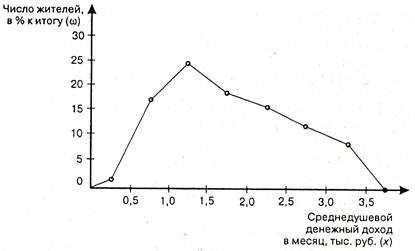
Рис.2. Полигон распределения населения по величине среднедушевого дохода
Кумулята распределения строится по накопленным частотам (частостям). Накопленные частоты (частости) определяют последовательным суммированием частот (частостей), они показывают, сколько единиц совокупности имеют значение признака не больше, чем рассматриваемое значение (гр. 4, табл. 1).
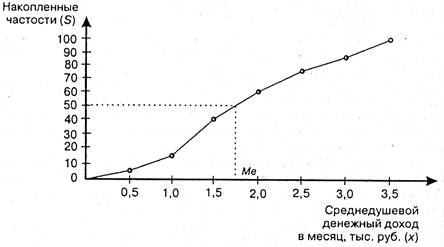
Рис.3.Кумулята распределения населения по величине среднедушевого дохода
При построении кумуляты интервального ряда (рис. 3) нижней границе первого интервала соответствует нулевая частота (частость), верхней - вся частота (частость) первого интервала. Верхней границе второго интервала – сумма частот (частостей) первого и второго интервалов и т. д. Верхней границе последнего интервала - сумма накопленных частот (частостей) во всех интервалах, что соответствует общей численности изучаемой совокупности или 100%.
Вывод по 1-му вопросу:
При изучении социально-экономических явлений и процессов статистика встречается с разнообразной вариацией признаков, характеризующих отдельные единицы совокупности. Величины признаков колеблются под воздействием различных причин. Возможно как табличное, так и графическое представление вариационного ряда.
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 817; Нарушение авторских прав?; Мы поможем в написании вашей работы!