Пространственно-временные характеристики

По пространственно-временным характеристикам определяют, как изменяются положения и движения человека во времени, как быстро человек изменяет свои положения (скорость) и движения (ускорение).

.1. Скорость точки и тела

Скорость точки¹ — это пространственно-временная мера движе­ния точки (быстроты изменения ее положения). Скорость равна первой производной по времени от расстояния в рассматриваемой системе отсчета:

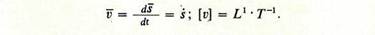
Скорость точки определяется по изменению ее координат во времени. Скорость — величина векторная, она характеризует быст­роту движения и его направление. Так как скорость движений человека чаще всего не постоянная, а переменная (движение неравномерное и криволинейное), для разбора упражнений определяют мгновенные скорости.

Мгновенная скорость — это скорость в данный момент времени или в данной точке траектории, скорость равномерного движения на очень малом участке траектории около данной точки траектории. Она равна первой производной пути по времени, тангенсу наклона касательной в данной точке траектории к выбранному направлению. Средняя скорость— это такая ско­рость, с которой точка в равномерном движении за то же время прошла бы весь рассматриваемый путь. Средняя скорость позволяет сравни­вать неравномерные движения.

Скорость точки (линейная) в прямолинейном движении направлена по траектории, в криволинейном— по касательной к траектории в каждой рассматриваемой ее точке.

Скорость тела определяют по скорости его точек. При поступательном движении тела линейные скорости всех его точек одинаковы по величине и направлению.

При вращательном движении определяют угловую скорость тела как меру быстроты изменения его углового положения. Она равна по величине первой производной по времени от углового перемещения:

Чем больше расстояние от точки тела до оси вращения (т. е. чем больше радиус), тем больше линейная скорость точки. Скорость вращательного движения твердого тела (в радианах) равна отношению линейной скорости каждой точки к ее радиусу (при постоянной оси вращения). Угловая скорость (ю) для всех точек тела, кроме лежащих на оси, одинакова:

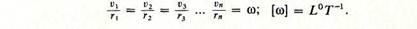
Значит, линейная скорость любой точки вращающегося тела, не лежащей на оси, равна его угловой скорости, умноженной на радиус вращения этой точки (расстояние от нее до оси вращения)

Скорость сложного движения твердого тела можно определить по линейной скорости любого полюса и угловой скорости вращения тела относи­тельно этого полюса (например, вокруг оси, проходящей через центр масс — ЦМ).

Скорость системы тел, изменяющей свою конфигурацию, В этом случае определяют линейную скорость ОЦМ системы и линейные скорости точек звеньев тела (проекций осей суставов на поверхность тела). При изменениях позы определяют угловые скорости звеньев тела относительно суставных осей; эти скорости обычно изменяются по ходу движения. Для биомеханического обоснования техники нужно в каждом случае вы­брать, какие скорости каких звеньев и точек следует определить.

Ускорение точки и тела

Ускорение точки — это пространственно-временная мера измене­ния движения точки(быстрота изменения движения — по величине и направлению скорости)

Различают ускорение линейное () и угловое ()

Линейное ускорение – равно первой производной линейной скорости по времени или второй производной пути по времени:

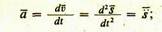
Ускорение — величина векторная, характеризующая быс­троту изменения скорости по ее величине и направлению в данный момент (мгновенное ускорение) К

Угловое ускорение тела определяется как мера быстроты изменения его угловой скорости. Оно равно первой производной по времени от угловой скорости тела:

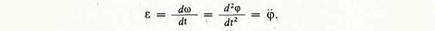
. Отношение ли­нейного ускорения каждой точки вращающегося тела к ее радиусу равно угловому ускорению (е) в радианах в секунду в квадрате. Оно одинаково для всех точек вращающегося тела, кроме лежащих на оси:

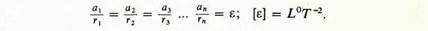
Значит, линейное ускорение любой точки вращающегося тела равно по величине его угловому ускорению, умноженному на радиус вращения этой точки:

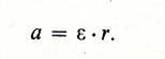
Вектор линейного ускорения во вращательном движении можно разложить на две составляющие:

а) касательное (тангенциальное),направленное вдоль касательной к траектории движения, характеризует изменение вектора скорости по модулю:

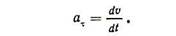
б) нормальное ускорение, перпендикулярное к вектору скорости и направленное вовнутрь кривизны траектории Нормальное ускорение характеризует изменение вектора скорости по направлению (рис 6)

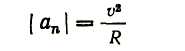
Касательное ускорение будет положительным, когда скорость точки возрастает

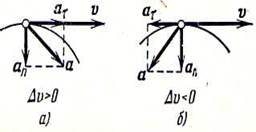
Рис 6.Разложение вектора ускорения на касательное и нормальное составляющие

Как видно из этого рисунка, величины а,а, а. связаны меду собой соотношением:

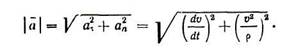
При этом:

:

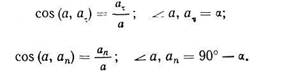
Дата добавления: 2014-01-03