Виды средних величин. Виды средних величин различаются прежде всего тем, какое свой­ство, какой параметр исходной варьирующей массы индивидуальных значений признака должны быть

Виды средних величин различаются прежде всего тем, какое свой­ство, какой параметр исходной варьирующей массы индивидуальных значений признака должны быть сохранены неизменными. Выбор средней в конкретном случае зависит от характера связи между вели­чиной признака, по значениям которого вычисляется средняя.

При прямой пропорциональности между определяющим свойст­вом и данным признаком, т.е. тогда, когда значения признака увели­чиваются и уменьшаются с увеличением или уменьшением характе­ризуемых ими явлений, всегда применяется средняя арифмети­ческая.

При изучении социально-правовых явлений наиболее часто ис­пользуются средняя арифметическая и средняя геометрическая.

Средняя арифметическая 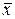вычисляется как сумма отдельных значений признака 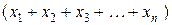, деленная на их число :

.

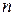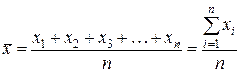Если, предположим, нужно вычислить средний возраст лиц, со­вершивших хулиганство (4 человека, возраст каждого из которых составляет 15, 16, 17, 18 соответственно), суммируются возрастные показатели каж­дого лица и сумма делится на число единиц совокупности.

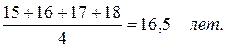
Однако этот простейший и всем известный способ определения средней применяется лишь тогда, когда каждая единица совокупности имеет различные значения изучаемого признака, т.е. его значения не повторяются.

Но возможны случаи, когда варианты признака могут быть одинаковые для целого ряда единиц совокупности. Число этих одинаковых вариантов называется весами, или частотами. В этих случаях вычисляется не простая, а взвешенная средняя арифметическая (с учетом весов конкретных вариантов при­знака):

.

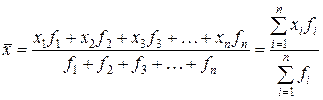где 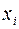- варианты и 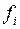- веса признака. Это и есть формула средней арифмети­ческой взвешенной.

Смысл средней взвешенной легко можно увидеть и на таком примере. Вычисляя средний возраст осужденных в ВК для несовер­шеннолетних, в которой содержатся 100 человек 15, 16, 17 и 18 лет, его, ко­нечно, нельзя определять исходя только из показателей приведенно­го вариационного ряда. Это приведет к ошибке.

Для правильного вычисления необходимо знать вес (частоту) указанных возрастных признаков, т.е. сколько человек каждой воз­растной группы находится в изучаемой совокупности.

Возраст (варианты)	Количество осужденных (вес каждого варианта)

Определим действительный средний возраст изучаемой совокупности:

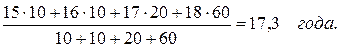
Из сопоставления полученных данных - 16,5 и 17,3 года - легко понять, почему между ними возникло расхождение. Дело именно в весе каждого варианта, поскольку больший вес (60 осуж­денных) имеет вариант 18 лет, он и «перетянул» среднюю в свою сторону.

На практике иногда встречается необходимость вычисления средней величины не из конкретных численных значений изучаемо­го признака, а из значений признака, сгруппированных в интервалы («от - до»).

Для решения такой задачи необходимо установить центры интервалов. Определив срединные значения интервалов, вычисляют обыч­ную среднюю взвешенную, т.е. центры интервалов умножают на веса и сумму произведений делят на сумму весов.

Средние арифметические показатели применяются для расчета среднегодового абсолютного прироста (снижения), выраженного в именованных числах. Они важны, но недостаточны, особенно в сравнительных целях, для достижения которых большую помощь ока­зывают темпы роста, прироста и снижения, выраженные в процентах, Расчет этих параметров производится по формуле средней геометриче­ской, но на основе тех же абсолютных показателей.

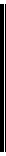Средняя геометрическая 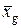вычисляется путем извлечения корня сте­пени 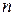из произведений отдельных значений признака:

,

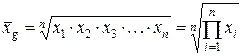где 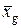- средняя геометрическая, 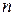- число значений признака, 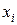- значения признака, 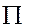- обозначение произведения.

Рассматриваемая величина используется для вычисления сред­них темпов роста и прироста (снижения) наблюдаемых явлений. Изучение этих параметров в динамике преступности, выявленных правонарушителей, раскрываемости, судимости, общего числа за­ключенных, оправданных, освобожденных от уголовной ответст­венности, рассмотренных гражданских дел, удовлетворенных и не­удовлетворенных исков и других меняющихся во времени юридиче­ски значимых явлений и процессов имеет важное практическое и научное значение.

Средняя арифметическая, средняя геометрическая и другие сред­ние — это своеобразная статистическая абстракция, поскольку они, отвлекаясь от истинных величин, отражают то общее, которое прису­ще всей совокупности изучаемых единиц в целом. Величина средних часто выражается дробными числами (22,6 правонарушителей, 105,8 исков и т.д.), которых в жизни не бывает. Наряду с ними в статистике используются структурные позиционные средние, величины которых занимают в ранжированном вариационном ряду, построен­ном в порядке возрастания или убывания значений вариант, опреде­ленное среднее положение. К таким средним относятся мода и медиа­на.

Медиану и моду используют в тех совокупностях, где расчет других средних невозможен или нецелесообразен.

Модой в статистике называется значение признака (варианта), ко­торое чаще всего встречается в данной совокупности.

Обозначим ее символом «Мо» и определим в вариационном ряду юридически значи­мых показателей (см. таблицу). Модой в данном примере будет варианта три дня, так как за этот срок было рассмотрено дел больше (85), чем за другие сроки.

В реальной жизни могут быть распределения, где все варианты встречаются примерно одинаково часто. В таких случаях мода не опре­деляется, так как она практически отсутствует. Мода применяется в тех изучениях, когда нужно охарактеризовать наиболее часто встречающуюся величину признака.

Дата добавления: 2014-01-03