Надежность элемента, работающего до первого отказа

Основные показатели надежности и математические методы их оценки

Задачи, изучаемые теорией надежности, делятся на 4 группы:

1. изучение природы возникновения отказов в элементах конструкций машин;

2. обеспечение качественной техдокументации на стадии проектирования;

3. обеспечение требуемого уровня надежности на стадии серийного производства;

4. поддержание регламентируемого уровня надежности на стадии эксплуатации.

В связи со случайным характером показателем работы машин и их элементов в качестве основы расчетного аппарата теории надежности используются методы математической статистики и теории вероятностей.

Типичная задача теории вероятности – предсказание результатов частного эксперимента исходя из некоторых общих закономерностей, характеризующих генеральную совокупность.

Типичная задача математической статистики – построение выводов характеризующих генеральную совокупность.

Модель события в момент 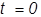элемент начинает работу, в момент 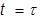происходит отказ. Значение 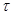заранее неизвестно.

Величина 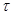может быть полностью описана с точки зрения теории вероятности функцией распределения 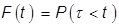, где P – коэффициент, характеризующий вероятность события 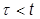; t – текущая переменная (координата времени или наработки).

В теории вероятности явление отказов при работе машины, получение определения размера детали при измерении, появление бракованного изделия при массовом изготовлении называется событием. Если событие может произойти, а может и не произойти, то оно называется случайным, а если оно обязательно должно произойти – то называется такое событие достоверным.

Два события называются несовместными, если при появлении одного, исключается появление другого.

Вероятностью события А называется отношение числа случаев, благоприятствующих наступлению данного события m ко всему числу несовместны, единственно возможных и равновозможных событий N.

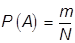
Если 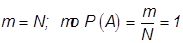, т.е. событие А достоверно.

Если 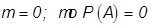- событие А невозможно.

Если появление одного из событий объективно не более возможно, чем другого, то такие события равновозможные.

Случайные величины, которые прине5мают лишь строго определенные значения называют дискретными, а случайные величины, принимающие любые значения величин в интервале – непрерывными.

Каждому значению случайной величины 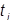соответствует частота появлений этого значения в эксперименте .

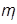Полное число испытаний .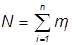

Отношения 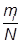есть частота и относительная частота появления i-го значения случайной величины.

Для непрерывных случайных величин определяет частота и частость попадания значений случайной величины в некоторые интервалы значений.

Функция 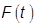есть вероятность отказа элемента до момента t, т.е. вероятность того, что величина 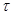принять меньшее значения, чем t. Предполагается, что функция 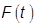непрерывна и дифференцируема, и следовательно существует непрерывная плотность распределения отказа .

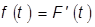Наряду с вероятностью отказа - 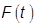используется также функция вида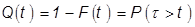

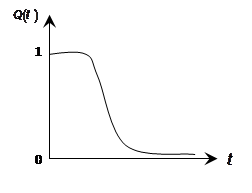
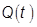- вероятность безотказной работы за время t. 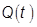называют такой функцией надежности.

По возможности получения большого числа наблюдений по срокам службы однотипных изделий, можно определить значения статистической функции распределения по накопленным частостям и построить график статистической функции 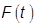, представляющей полигон накопленных частостей 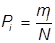, где N – число всех наблюдаемых случаев рассматриваемой выбором из общей генеральной совокупности; 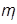- частота повторения одинаковых результатов в принятом интервале времени.

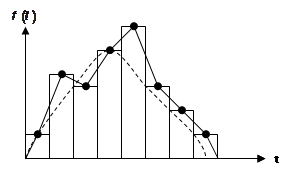Распределение частостей непрерывной случайной величины характеризуется гистограммой.

По оси абсцисс весь интервал значений разбивается на единичные интервалы. На них строятся прямоугольники, площадью равные частостям попадания случайных величин в эти единичные интервалы. Соединяя ординаты середин интервалов на гистограмме, получаем полигон распределения. Аппроксимируя полигон некоторой кривой, получаем кривую плотности распределения (плотность вероятности) 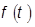. Вероятность попадания случайной величины в интервал .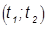

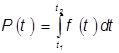Плотность вероятности есть предел отношения вероятности того, что случайная величина T примет значение лежащее между 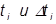к величине интервала 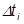при 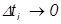, т.е.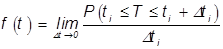

По эмпирическим гистограммам, полигонам и плотностям и кривым распределения подбираются теоретические кривые распределения.

Статистическая оценка вероятности безотказной работы в пределах наработки от 0 до t имеет вид 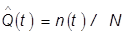, где n – число изделий не отказавших по времени t.

Статистическая оценка плотности вероятности безотказной работы 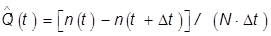, где 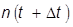- число исправных элементов в конце интервала Dt.

В практических задачах нет необходимости характеризовать случайную величину полностью. Достаточно указать только отдельные числовые параметры, характеризующие существенные стороны распределения случайной величины.

Дата добавления: 2014-01-03