Дискретные случайные величины. 1. Число гербов, выпавшее при 10 бросаниях монеты

Примеры случайных величин.

1. Число гербов, выпавшее при 10 бросаниях монеты.

2. Количество попаданий при 10 выстрелах.

3. Число произведенных выстрелов при стрельбе до первого попада­ния.

4. Длина листа, сорванного с конкретного дерева.

5. Время ожидания автобуса на остановке.

Очевидно, что для задания случайной величины просто перечислить все её значения мало, а порой и невозможно. Более того, случайные величины в примере 1 и 2 принимают одинаковые перечни возможных значений, однако вероятности у них различные.

Разнообразие случайных величин весьма велико. Число принимаемых значений может быть конечным или бесконечным, значения могут быть расположены на числовой оси дискретно или заполнять некоторые интервалы целиком. В зависимости от этого свойства случайные величины принято разделять на дискретные и непрерывные.

Интуитивно ясно, что возможные значения дискретной случайной величины есть отдельные изолированные числа, которые эта величина принимает с определенными вероятностями, а значения непрерывной случайной величины заполняют целиком некоторые интервалы.

Дискретной называется случайная величина, которая может принимать конечное или счетное множество различных значений (счетным называется множество, все элементы которого можно поставить во взаимнооднозначное соответствие с числами натурального ряда, т.е. перенумеровать.). В примерах 1-3 рассмотрены дискретные случайные величины.

Рассмотрим сначала случайные величины, которые могут принимать лишь конечное число различных значений.

Пусть возможными исходами некоторого эксперимента являются события 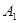, , 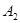… , 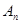которые образуют полную группу попарно несовместных событий. Пусть 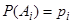(т.е. вероятность появления события А_i в результате эксперимента равна 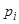). Заметим, что .

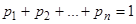Введем некоторую числовую функцию x, которая ставит в соответствие событиям числа: 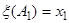, , 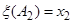…, 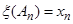. Таким образом, мы определили значения, которые может принимать случайная величина x: если наступило событие А_i, то случайная величина принимает значение x_i .

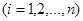Этот факт может быть записан следующим образом: 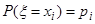(вероятность того, что случайная величина принимает значение x_i, равна ).

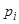Теперь вместо того, чтобы говорить «события 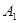, , 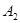… 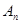образуют полную группу попарно несовместных событий и происходят в результате эксперимента с вероятностями 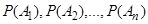», можем сказать «задана случайная величина x, которая принимает значения 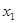, , 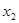… 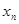с вероятностями , , … ».

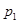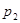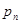Набор 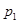, , 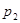… 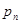называется распределением вероятностей случайной величины x.

Случайную величину x удобно задавать в виде таблицы:

x	x1	х2	…	х n
p	p1	p 2	…	pn

Эта таблица называется законом распределения величины x.

Дата добавления: 2014-01-03