Зависимость главного вектора от выбора центра приведения

Лекция 8

Пусть задача произвольная пространственная система сил 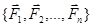, приложенных к твердому телу (рис.8.1). При приведении заданной системы 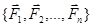к центру О получаем эквивалентную систему, характеризуемую главным вектором .

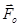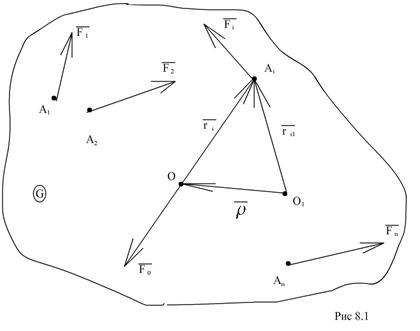
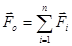
И главным моментом М_о: 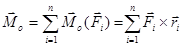. Приведем заданную систему к новому центру приведения О₁. Главный вектор системы не измениться, главный момент изменится, поскольку относительно нового центра приведения момент каждой из сил системы станет другим. Найдем эго изменение. Пусть 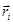- радиус вектор точки приложения силы 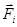приведенный из центра О₁

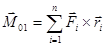, где

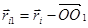
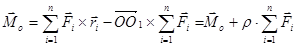
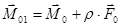(8.1)

Вывод: при изменении центра приведения главный момент изменится на величину равную моменту главного вектора приложенного в старом центре приведения относительно нового центра приведения.

Статические инварианты

Главный вектор системы не изменяется при перемене центра приведения. Эту величину называют первым статическим инвариантом пространственной системы сил по отношению к изменению центра приведения.

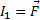(8.2)

Вторым статическим инвариантом является скалярное произведение главного вектора на главный момент. Умножая обе части выражения (8.1) на главный вектор 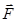получаем:

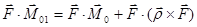
Но второй член правой части этого выражения будет равняться нулю:

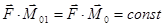
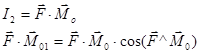(8.3)

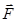является инвариантом, поэтому (8.3) можно записать:

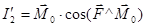(8.4)

Скалярное произведение главного вектора 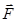на главный момент М_о (т.е. величина определяемая выражением (8.3)) или проекция главного момент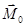а на 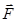(т.е. величина определяемая (8.4)) постоянны для данной системы сил и не зависят от выбора центра приведения, а поэтому является вторым статическим инвариантом системы т.к. центр приведения О – выбран произвольно, то главный вектор 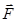и главный момент М_о будет составлять между собой некоторый угол 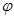отличный от О:

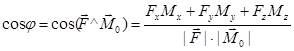(8.5)

Доказательство

Пусть пространственная система сил 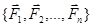имеет равнодействующую 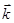и точку О лежит на линии действия равнодействующей. Если приводить систему сил к этой точке, то главный момент:

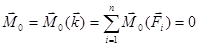
Выберем теперь другую точку О₁, как центр приведения, для этого центра приведения главный момент заданной системы сил будет равен:

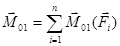
С другой стороны, на основании формулы 8.1 имеем:

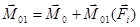(8.6)

Учитывая, что М₀=0, а 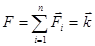, из 8.6 получаем:

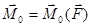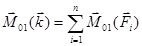или (8.7)

Теорема доказана.

Дата добавления: 2014-01-03