Лекция № 6

Тема: биномиальные коэффициенты

Основные вопросы, рассматриваемые на лекции:

1. Формула бинома Ньютона.

Свойства биномиальных коэффициентов:

2. Следствия формулы числа сочетаний без повторений;

3. Следствия формулы бинома Ньютона.

Краткое содержание лекционного материала

1. Формула бинома Ньютона. Бином Ньютона (1+ x) ⁿ, после раскрытия скобок и приведения подобных, преобразуется в многочлен канонического вида a ₀ xⁿ + a ₁ x^{n -1}+…+ a_{n -1} x ¹+ a_nx ⁰, где a ₀=1, a_n =1, x ⁰=1. Оказывается, что 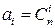, где i =0,1,…, n. Поэтому числа сочетаний 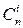называются также биномиальными коэффициентами. Применятся обозначение: 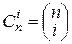. Формула в следующей теореме называется формулой бинома Ньютона или биномом Ньютона.

Теорема 1. .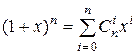

Доказательство. 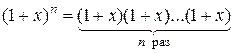. Раскроем скобки и приведем подобные: в полученном многочлене коэффициент при степени xⁱ равен сумме i единиц и n -i нулей. Число всевозможных выборов i единиц из общего числа выборов n равно .

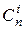2. Свойства биномиальных коэффициентов как следствия формулы числа сочетаний без повторений. Используя формулу теоремы 5 лекции №5, можно доказать свойства биномиальных коэффициентов, которые мы приведем в следующей теореме.

Теорема 2. , , .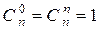

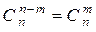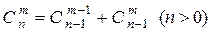Доказательство. . .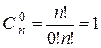

.

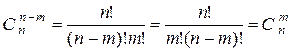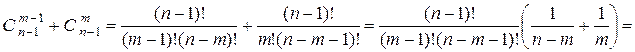
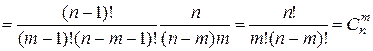Задача 1. Найти все биномиальные коэффициенты для .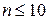

Решение запишем в виде треугольника Паскаля – бесконечной таблицы, имеющей треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы, так как 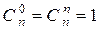. Каждое внутреннее число равно сумме двух расположенных над ним чисел: 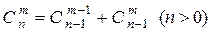. Строки треугольника симметричны относительно вертикальной оси: .

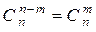Биномиальный коэффициент 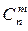лежит на пересечении строки n и столбца m.

m n

3. Свойства биномиальных коэффициентов как следствия формулы бинома Ньютона. Используя формулу теоремы 1, можно доказать свойства биномиальных коэффициентов, которые мы приведем в следующей теореме.

Теорема 3. Имеют место следующие тождества:

1) ;

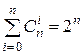2) ;

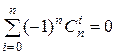3) ;

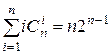4) .

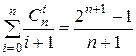Доказательство. 1) В тождестве теоремы 1 подставим x =1.

2) В том же тождестве подставим x =-1.

3) Продифференцируем обе части того же тождества по x:

.

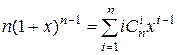Затем подставим x =1.

4) Проинтегрируем обе части того же тождества по x от 0 до 1:

.

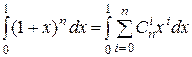Получим: .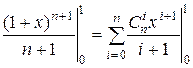

Дата добавления: 2014-01-03