Определение функции

Функции

ДО 5 БАЛЛОВ ЗА КОНСПЕКТ

Определение. Функцией называют бинарное отношение 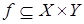, обладающее следующим свойством: есл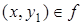и и 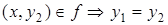. Это означает, что если определён первый элемент упорядоченной пары, то второй элемент определяется единственным образом.

Такое свойство функции называют однозначностью. Говорятеще, чтодля функции выполнено условие однозначности. Обозначения функции: 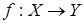, , 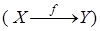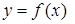. Функция f отображает множество 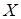в множество Y.

Если y = f (x), то элемент x из множества Х называют аргументом функции или прообразом элемента y, а элемент y – значением функции или образом элемента x.

В силу условия однозначности у всякого прообраза есть единственный образ.

Аргументы функции - элементы произвольной природы. В частности, они могут быть упорядоченными энками, 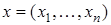. В этом случае функцию 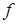называют функцией 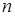переменных и пишут: 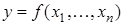. Функция двух переменных 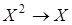в некоторых случаях называется бинарной операцией.

Областью определения 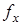функции f называют множество ее аргументов (прообразов), 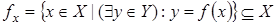. Если область определения совпадает с Х, то функция называется тотальной, в противном случае функция называется частично определенной.

Областью значений 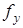функции f называют множество ее значений (образов), 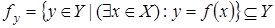Если область значений совпадает с множеством Y, функция называется сюръекцией или сюръективной.

О сюръективной функции говорят, что она отображает множество Х на множество Y.

Пример.

Определить, какие из приведенных бинарных отношений являются функциями.

1.{(1, 1), (1, 2), (2, 4), (3, 6)}; 2. {(1, 1), (2, 4), (3, 4)};

3.{(x, y) | x = y ², x, y Î R }; 4. {(x, y) | y = x ², x, y Î R }.

Решение.

1. Это бинарное отношение, не функция, нарушено условие однозначности. В бинарное отношение входят две разные упорядоченные пары – (1, 2) и (1, 1) с одинаковым первым элементом.

2. Данное бинарное отношение – функция с областью определения {1, 2, 3} и множеством значений {1, 4}.

3. Отношение {(x, y) | x = y ², x, y Î R } функцией не является. В него входят, например, упорядоченные пары (4, 2) и (4, -2).

4. Задана функция y = x ². Значение у единственным образом определяется по значению аргумента х.

Определение. Функция 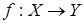называется инъективной или инъекцией, если 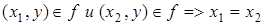. Другими словами, у каждого образа есть единственный прообраз.

Определение. Функция 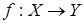называется биективной или биекцией, если она одновременно инъективна и сюръективна. Биекцию по-другому называют взаимно однозначным соответствием между областью определения и областью значений; каждому элементу x из области определения функция f ставит в соответствие единственный элемент y из области значений и наоборот, для каждого y Î Y существует единственный x Î X.

Проиллюстрируем введенные определения.

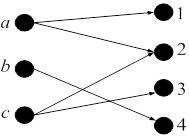
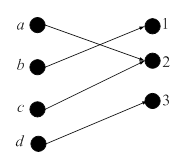
Рис. 1. Бинарное отношение, Рис. 2. Сюръекция, но не

но не функция инъекция

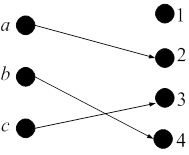
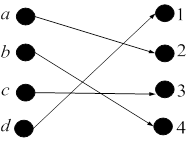
Рис. 3. Инъекция, но не Рис. 4. Тотальная биекция

сюръекция

Так как функция – это бинарное отношение, можно построить обратное бинарное отношение 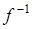, которое не обязательно является функцией. Условие однозначности может быть нарушено.

Дата добавления: 2014-01-03