Лекция 8. В этом многочлене два первых коэффициента при старших степенях λ определяются лишь произведением элементов главной диагонали определителя

.

В этом многочлене два первых коэффициента при старших степенях λ определяются лишь произведением элементов главной диагонали определителя 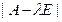, т.е. выражением вида:

.

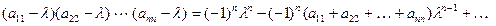Так что с точностью до знак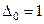а , а 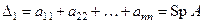– след матрицы А, т.е. сумма диагональных элементов матрицы А. Легко найти также 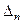. Из уравнения (€) видно, что если принять 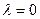, то .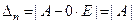

Всякий вещественный корень уравнения (€) будет собственным значением оператора А. Этому собственному значению будут соответствовать собственные (ненулевые) векторы оператора А (их может быть больше одного), координатные столбцы которых найдутся из уравнения .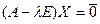

Комплексным корням уравнения (€) с точки зрения линейных пространств, в которых рассматривается умножение векторов лишь на действительные числа, не будут соответствовать никакие собственные векторы.

Что будет происходить с собственными значениями и собственными векторами при смене базиса? Оказывается, характеристический многочлен 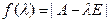не меняется при смене базиса. Действительно, пусть в другом базисе этот многочлен имеет вид 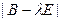. Но матрицы оператора в разных базисах связаны равенством 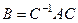, где С – невырожденная матрица. Тогда имеем:

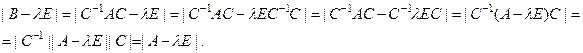
Значит, собственные значения оператора А не зависят от того, в каком базисе они вычислены по матрице этого оператора. Соответственно, не зависят от базиса и собственные векторы.

Одному собственному значению может соответствовать несколько собственных векторов, но один и тот же собственный вектор не может соответствовать разным собственным значениям.

Собственные векторы, соответствующие одному собственному значению 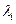, образуют так называемое собственное подпространство 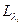, т.е. множество всех тех векторов z, которые удовлетворяют равенству 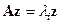. Действительно, пусть x и y – собственные векторы, соответствующие одному собственному значению 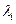. Тогда имеем: 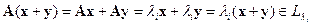, а также для произвольного значения .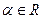

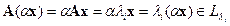Размерность 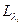не превышает кратности 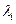как корня характеристического многочлена. Это последнее утверждение требует доказательства.

Пусть размерность 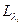равна т. Выберем базис в L так, чтобы первые т его векторов были из 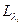. Остальные 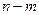базисных векторов будут выбраны из оставшейся части L. В этом базисе матрица оператора А будет иметь вид (по построению матрицы оператора – ее столбцы есть координатные столбцы векторов, в которые оператор переводит базисные векторы):

,

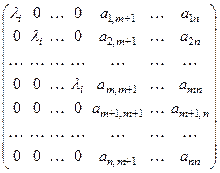и характеристическое уравнение будет выглядеть так: 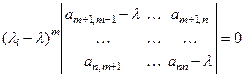. Таким образом, кратность корня 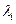равна по меньшей мере т (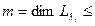кратность ). ■

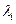Если ненулевые собственные значения 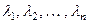попарно различны и их число совпадает с размерностью пространства L, то говорят, что линейный оператор обладает простым спектром.

Теорема 4.2. Система собственных векторов 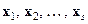, отвечающих попарно различным собственным значениям оператора А, линейно независима.

Док-во (индукцией по числу векторов).

Если 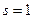, то справедливость теоремы очевидна, т.к. .

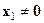Положим далее, что теорема верна для 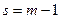и докажем, что она верна для 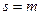. Предположим противное, т.е., что существует нетривиальная линейная комбинация, равная 0:

(а) .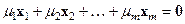

Пусть, например, 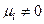. Применим к этому равенству оператор А:

(б) .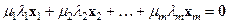

Умножая выражение (а) на 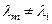и вычитая получившееся равенство из (б), получим:

.

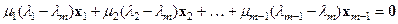Отсюда 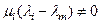, т.к. 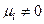и 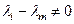, по условию теоремы. Но это означает, что построена нетривиальная комбинация для линейно независимых векторов 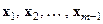, что противоречит индуктивному предположению об их линейной независимости. ■

Т.к. характеристическое уравнение не может иметь больше п различных корней, то в соответствии с теоремой 4.2 пространство L не может иметь более п собственных векторов с попарно различными собственными значениями. Если теперь перейти в L к базису, состоящему из этих линейно независимых собственных векторов 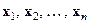, то матрица 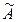линейного оператора в этом базисе (по построению матрицы линейного оператора) будет иметь диагональный вид:

.

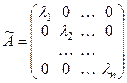Какая матрица С потребуется для смены базиса, при которой матрица оператора примет такую диагональную форму? Для этого преобразуем равенство 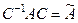, умножив его слева на С: 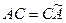. Рассмотрим j- й столбец 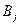матрицы 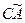: 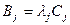, где 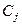– j- й столбец матрицы С. В произведении АС ему соответствует произведение 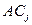. Отсюда получаем равенство 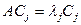. Оно говорит о том, что столбцы 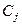являются собственными векторами оператора А, соответствующими собственному значению .

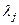Пример. Найти собственные значения и соответствующие им собственные векторы (координатные столбцы) для матрицы оператора 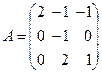. Построить матрицу 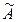оператора в базисе из собственных векторов, после чего найти матрицу, в соответствии с которой меняется базис.

Характеристическое уравнение: .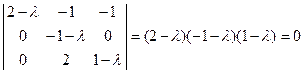

Имеем 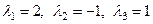(простой спектр). Находим собственные векторы-столбцы.

Для : , .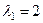

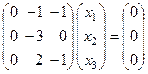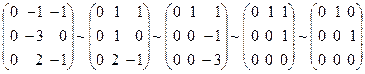Отсюда .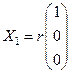

Для : , .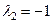

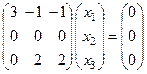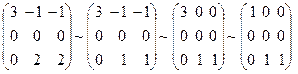Отсюда .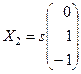

Для : , .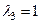

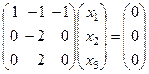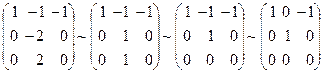Отсюда .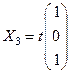

Матрица оператора в базисе из собственных векторов имеет вид: .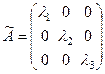

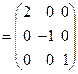Для 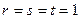(не единственная комбинация!) из векторов 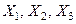как из столбцов строим матрицу 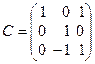, связывающую новый базис 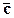со старым: 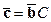(проверьте выполнение равенства ).

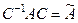Дата добавления: 2014-01-03