Определение сопряженных глубин

Деление

Умножение

При умножении двух нормализованных чисел их порядки складываются, а мантиссы перемножаются.

Пример 3. Выполнить умножение двоичных нормализованных чисел:

(0.11101 ^. 2¹⁰¹) ^. (0.1001 ^. 2¹¹) = (0.11101 ^. 0.1001) ^. 2^(101+11) = 0.100000101 ^. 2¹⁰⁰⁰.

При делении двух нормализованных чисел из порядка делимого вычитается порядок делителя, а мантисса делимого делится на мантиссу делителя. Затем в случае необходимости полученный результат нормализуется.

Пример 4. Выполнить деление двоичных нормализованных чисел:

0.1111 ^. 2¹⁰⁰: 0.101 ^. 2¹¹ = (0.1111: 0.101) ^. 2^(100-11) = 1.1 ^. 2¹ = 0.11 ^. 2¹⁰.

Использование представления чисел с плавающей точкой существенно усложняет схему арифметико-логического устройства.

Практическая часть – запустить через сетевое окружение электронный учебник по информатике

Литература

Электронный вариант учебника Шауцуковой по информатике.

Если одна из сопряженных глубин известна, то вторую можно найти решая:

1. аналитически уравнение гидравлического прыжка.

2. методом подбора

3. по графику прыжковой функции.

Решим уравнение гидравлического прыжка для прямоугольного сечения:

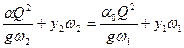|ω=bh; y=h/2|

_;

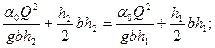
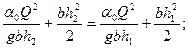
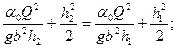
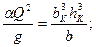
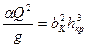
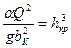
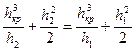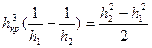
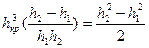
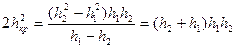
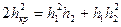
Это уравнение симметрично относительно глубин до прыжка и после прыжка.

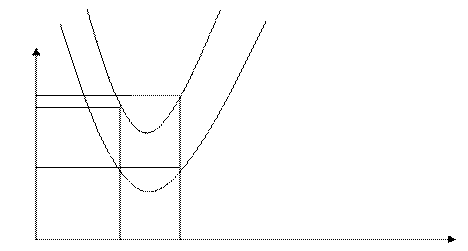Потери энергии в гидравлическом прыжке.

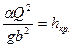
l(h)

П(h)

l₁

l₂

П(h)

П(h₁)

0 h₁ h₂ h

Когда происходит гидравлический прыжок между двумя сопряженными глубинами h₁ и h₂ наблюдается уменьшение скорости движения жидкости, вращение отдельных частиц, а так же пульсация. Что приводит к потерям энергии. То есть наблюдается явления аналогичные тем, что происходят в местных сопротивлениях. Если совместить график П(h) и график удельной энергии сечения, то мы получим, что энергия на глубине h₂ всегда меньше, чем на глубине h₁. То есть при гидравлическом прыжке наблюдаются потери энергии и их можно определить.

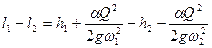
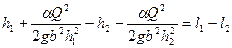
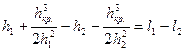
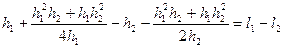
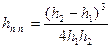Из него следует, что чем больше высота, тем больше потери энергии в таком прыжке.

Дата добавления: 2014-01-03