Первый закон Зипфа

Законы Зипфа

Оказывается, все созданные человеком тексты построены по единым правилам! Никому не удается обойти их. Какой бы язык ни использовался, кто бы ни писал - классик или графоман, - внутренняя структура текста останется неизменной. Она описывается законами Зипфа (G.K. Zipf).

Выберем в тексте любое слово и посчитаем, сколько раз оно встречается в тексте. Эта величина называется частотой вхождения слова. Измерим частоту вхождения каждого слова текста. При этом некоторые слова будут иметь одинаковую частоту, то есть входить в текст равное количество раз. Объединим слова с одинаковой частотой вхождения в одну группу. Расположим частоты по мере их убывания и пронумеруем. Порядковый номер частоты назовём рангом частоты. Так, наиболее часто встречающиеся слова будут иметь ранг 1, следующие за ними - 2 и т. д. Определим вероятность вхождения конкретного слова в текст. Вероятность будет равна отношению частоты вхождения этого слова к общему количеству всех слов в тексте.

Вероятность = Частота вхождения слова / Количество слов в тексте

Джорж Зипф (G. K. Zipf) в 1949 году обнаружил интересную закономерность. Оказывается, если умножить вероятность вхождения слова в текст на ранг частоты, то получившаяся величина (С) приблизительно постоянна:

С = (Частота вхождения слова х Ранг частоты) / Количество слов в тексте = const

Преобразовав эту формулу к виду:

Частота вхождения слова = (Количество слов в тексте х С) / Ранг частоты,

и учитывая, что не только C, но и количество слов в конкретном тексте – величины постоянные, легко заметить, что функция Частота вхождения слова(Ранг частоты) есть функция вида y=k/x (где k=const, x – аргумент функции y) и ее график - гипербола, представленная на рисунке 1. Следовательно, по первому закону Зипфа, если самое распространенное слово встречается в тексте, например, 100 раз (соответствует значениям y = 100/1), то следующее по частоте слово вряд ли встретится 99 раз. Частота вхождения второго по популярности слова, с высокой долей вероятности, окажется около 50 (y = 100/2), третьего – около 33 (y = 100/3), четвертого – около 25 (y =100/4) и т. д. Значение константы С в разных языках различно, но внутри одной языковой группы остается неизменно, какой бы текст мы ни взяли. Так, например, для английских текстов константа Зипфа равна приблизительно 0,1, для русского языка - 0,06-0,07.

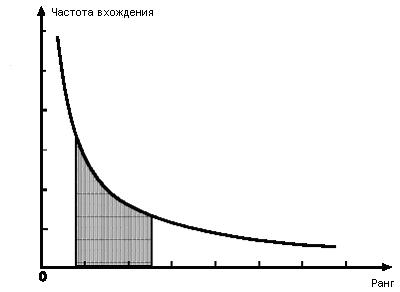
Рисунок 1 - Зависимость Частоты вхождения слова от Ранга частоты

Дата добавления: 2014-01-03