
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Алгоритм распознавания распределения Гаусса по ГОСТ 11.006-74
|
|
|
|
| 1. База данных эксперимента (xi, Pi), n>20, X, S, tnP, |
| 2. Расчет числа данных (G), вышедших за интервал Х±0.3*S |
| 3. Если G*20/n2<=0.741*tnP, то распределение Гауссово |
Критерии и алгоритмы обнаружения глобального экстремума при распознавании распределения Гаусса.
Функция имеет глобальное решение при любых 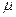 и
и 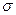 . Расчет критерия оптимизации U =
. Расчет критерия оптимизации U = 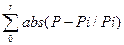 .
.
Алгоритм распознавания распределения Гаусса (оценка 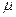 и
и 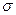 )
)
| 1. База данных эксперимента (xi, Pi) |
2. Оценка 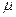 по xi = max. Если имеется два одинаковых max значений, то выбирается среднее значение по xi = max. Если имеется два одинаковых max значений, то выбирается среднее значение 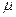
|
3. Оценка 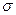 по Рxi=max./2 и обнаружением хi соответствующих или близких к Рxi=max./2, а далее нахождением половины разницы между ними по Рxi=max./2 и обнаружением хi соответствующих или близких к Рxi=max./2, а далее нахождением половины разницы между ними
|
4. Расчет P=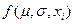
|
5. Расчет критерия оптимизацииU = 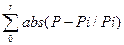 . Установление знака градиента изменения . Установление знака градиента изменения 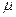 и и 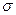 . Установление шага изменения . Установление шага изменения 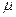 и и 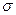 по золотому сечению. по золотому сечению.
|
6. Поиск решения при совместном переборе значений 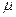 и и 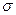 методом безинерционного шарика методом безинерционного шарика
|
7. Изменение 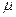 и и 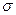 до ухудшения критерия U до ухудшения критерия U
|
| 8.Повтор итерации с изменением шага градиента на порядок и изменением знака градиента |
| 9. Определение предельного числа итераций вручную при достижении незначимости изменения критерия оптимизации или автоматический выход из расчетов при достижении заданной точности U |
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 752; Нарушение авторских прав?; Мы поможем в написании вашей работы!