
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Другие распределения
|
|
|
|
| Название | Уравнение | Особенности | Примеры |
| Хи-квадрат | 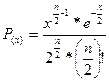
| Таблицы распределения задаются в виде процентных точек, задаваемых условием 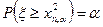
| Используется при построении доверительных интервалов для оценок дисперсии. |
| Стьюдента | 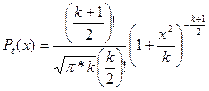 ,
k=n-1, ,
k=n-1, 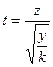
| Так распределена СВ, t, где z- распределено нормально (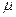 =0, =0,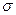 =1); y- имеет распределение хи-квадрат с k степенями свободы =1); y- имеет распределение хи-квадрат с k степенями свободы
| Используется при определении доверительных интервалов среднего арифметического при экспериментально оцениваемой дисперсии. |
| Фишера | 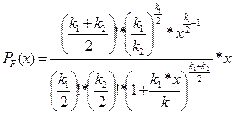 , ,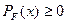
| Так распределена СВ 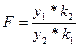 ,где ,где 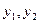 -имеют распределение хи- квадрат с -имеют распределение хи- квадрат с 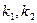 степенями свободы соответственно. степенями свободы соответственно.
| Используется при дисперсионном анализе |
| Рэлея | 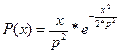 , ,
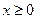
| Имеет модуль двумерного вектора, координаты которого распределены нормально с нулевым средним и равными 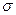
| Для аппроксимации распределения контролируемых показателей, которые могут быть только одного знака. |
| Равномерное | 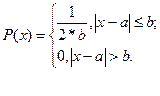
| Имеет погрешность округления | Обладает наибольшей неопределенностью для всех СВ, принимающих значение в интервале (a-b;a+b). Во многих случаях может рассматриваться как крайний случай, как наихудшее распределение. |
| Арккоси-нусное | 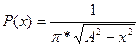 , ,
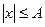
| Такое распределение имеют отсчеты гармонического колебания с равномерно распределенной начальной фазой. Также значения контролируемых параметров, которые в процессе изготовления подвергаются регулированию. |
Критерии и алгоритмы обнаружения глобального экстремума при распознавании распределения Пуассона (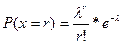 ). Функция имеет глобальное решение при
). Функция имеет глобальное решение при 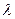 > 0. Расчет критерия оптимизации U =
> 0. Расчет критерия оптимизации U = 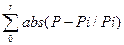
Алгоритм расчета 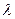
|
| 1. База данных эксперимента (xi, Pi) |
2. Оценка 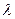 по xi = max. по xi = max.
|
| 3. Расчет факториала при заданном r |
4. Поиск решения значения 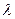 аналогично п. 4- 9 таблицы 6 аналогично п. 4- 9 таблицы 6
|
Нельзя задавать значение r большей экспериментальной.
Критерии и алгоритмы обнаружения глобального экстремума при распознавании распределения Коши (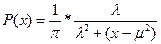 ). Функция имеет глобальное решение при
). Функция имеет глобальное решение при 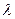 > 0. Расчет критерия оптимизации U =
> 0. Расчет критерия оптимизации U = 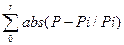
Алгоритм расчета 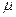 и и 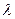
|
| 1. База данных эксперимента (xi, Pi) |
2. Оценка 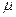 по xi = max. по xi = max.
|
2. Оценка 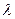 по «полуширине» экспериментальной функции распределения. В случае если теоретическая кривая с оцененными значениями по «полуширине» экспериментальной функции распределения. В случае если теоретическая кривая с оцененными значениями 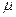 и и 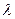 выше экспериментальной, то выше экспериментальной, то 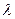 дополнительно умножается на коэффициент более 1 (обычно на 6) дополнительно умножается на коэффициент более 1 (обычно на 6)
|
3. Поиск решения при совместном переборе значений 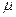 и и 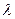 аналогично п. 4- 9 таблицы 6 аналогично п. 4- 9 таблицы 6
|
|
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 301; Нарушение авторских прав?; Мы поможем в написании вашей работы!