Аналитическое выражение второго закона термодинамики

Если изолированная система находится в неравновесном состоянии, то в ней всегда происходят самопроизвольные необратимые процессы, приближающие ее к состоянию равновесия. Как это было показано выше, энтропия всей системы в целом при этом увеличивается, а энергия ее, не изменяясь количественно, деградирует качественно, т.е. работоспособность системы по мере протекания в ней необратимых процессов уменьшается.

В конечном итоге система приходит в состояние равновесия, самопроизвольные необратимые процессы в ней прекращаются, а энтропия перестает увеличиваться, т.е. достигает своего максимума. Это означает, что условия равновесия системы могут быть выражены аналитически условиями максимума ее энтропии, т.е. соотношениями

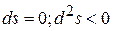. (5.32)

В связи с этими соображениями второй закон термодинамики, устанавливающий необратимость и одностороннюю направленность всех самопроизвольных процессов в неравновесных системах может быть сформулирован так: энтропия неизолированной равновесной системы стремится к максимуму, достигая его, когда самопроизвольные процессы в ней прекращаются и система приходит в состояние равновесия.

Эта формулировка показывает, что энтропия системы представляет собой параметр, изменение которого отражает не только качественные, но и количественные ограничения, накладываемые на тепловые процессы вторым законом термодинамики. В наиболее общей форме эти ограничения описываются формулой

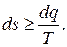, (5.33)

которая и является, таким образом, аналитическим выражением второго закона термодинамики.

Применительно к неизолированным системам знак равенства показывает, что все процессы обмена энергией между системой и окружающей средой обратимы, а знак неравенства свидетельствует о наличии и необратимых процессов. Применительно к изолированным системам, для которых dq = 0 и, следовательно, аналитическое выражение второго закона термодинамики принимает вид ds ≥ 0, знак равенства показывает, что в системе необратимые процессы отсутствуют, а знак неравенства свидетельствует о наличии в ней необратимых процессов.

Аналитическому выражению второго закона термодинамики можно придать вид:

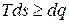, (5.34)

а поскольку по первому закону термодинамики

,

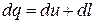любой термодинамический процесс должен удовлетворять соотношению

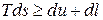, (5.35)

которое является, таким образом, объединенным аналитическим выражением первого и второго закона термодинамики. Как ясно из предыдущего, знак равенства относится к обратимым процессам, а знак неравенства – к необратимым.

Дата добавления: 2014-01-03