Термические коэффициенты

Как и у идеального газа, каждый из основных параметров р,J и Т, являясь функцией состояния реального газа, определяется значениями двух других параметров и может быть найден из уравнения

,

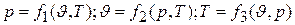которые являются различными формами уравнения состояния.

Таким образом, два любых параметра могут быть приняты за независимые переменные, определяющие значение третьего параметра, а следовательно, и всех других термодинамических величин, являющихся функциями состояния газа.

При этих условиях выше приведенные уравнения состояния в дифференциальной форме будут иметь вид

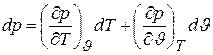, (6.4)

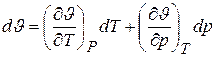, (6.5)

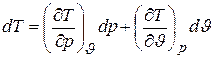, (6.6)

где dp,dJ, dT – полные дифференциалы соответствующих параметров.

В указанные уравнения входят шесть частных производных, которые попарно обратны друг другу, например

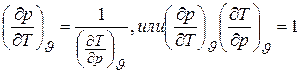. (6.7)

Следовательно, самостоятельное значение из шести частных производных имеют только три. В качестве основных применяются частные производные

,

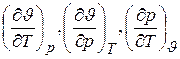которые называются термическими коэффициентами. Каждый из термических коэффициентов имеет определенное физическое содержание.

Так, частная производная 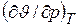характеризует интенсивность изменения объема при изменении давления в условиях постоянной температуры. Отношение этой величины к начальному объему газа J₀, взятое с обратным знаком, называется коэффициентом сжатия

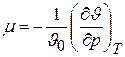. (6.8)

Термический коэффициент 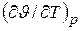характеризует интенсивность увеличения объема при нагревании при постоянном давлении. Отношение этой величины к начальному объему, т.е.

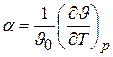, (6.9)

называется коэффициентом объемного расширения.

Наконец, термический коэффициент 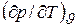характеризует интенсивность изменения давления при изохорном нагреве тела. Отношение этой величины к начальному давлению р₀, т.е.

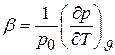, (6.10)

называется коэффициентом упругости.

Названные коэффициенты связаны между собой весьма простым соотношением. Найти это соотношение можно следующим образом.

Из математики известно, что если переменные x,y и z связаны между собой уравнением

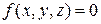
и не зависит от каких – либо других переменных, то их частные производные удовлетворяют тождеству

.

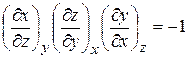Применив это положение к уравнению состояния

,

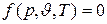получаем

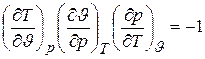
или ,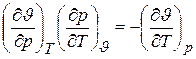

т.е уравнение связи между термическими коэффициентами.

Далее, учитывая, что

,

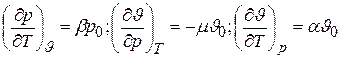находим

,

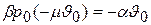или окончательно

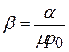. (6.11)

Эта формула позволяет теоретически определить коэффициент упругости, нахождение которого опытным путем затруднительно, в то время как коэффициенты a и m легко определяются экспериментально.

Дата добавления: 2014-01-03