Сложение гармонических колебаний

Метод векторных диаграмм.

Гармонические колебания изображаются графически методом вращающегося вектора амплитуды, или методом векторных диаграмм.

Для этого из произвольной точки О, выбранной на оси х, под углом φ, равными начальной фазе колебания, откладывается вектор А, модуль которого равен амплитуде колебания.

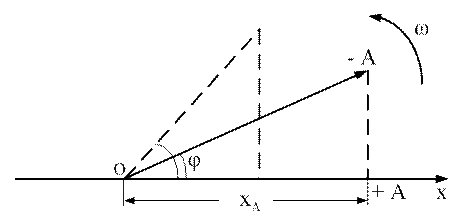
Если этот вектор А привести во вращательное движение с угловой скоростью ω, то проекция этого вектора х_А на ось х будет перемещаться по оси х и принимать значения от +А до –А, а колеблющаяся величина будет изменяться по закону синуса или косинуса.

.

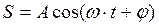Отсчет угла фазы колебания ведется от оси х в направлении против часовой стрелки.

Одно тело может участвовать в нескольких колебательных движениях, которые необходимо сложить и найти результирующее колебание.

Сложим 2 гармонических колебания.

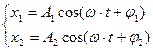
С одинаковыми частотами 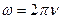, разными амплитудами А₁ и А₂ и разными начальными фазами φ₁ и φ₂.

представим колебания в виде векторных диаграмм и сложим их по правилу сложения векторов.

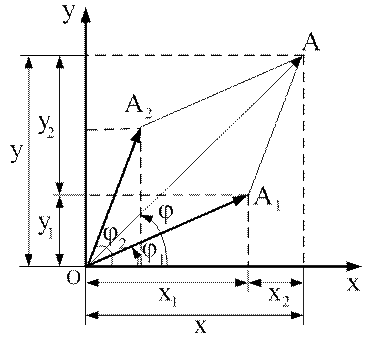
Результирующему суммарному колебанию соответствует вектор А проекция которого на ось х:

х = х₁ + х₂ – проекция А на ось х.

Само результирующее колебание х = А cos (ωt+φ)

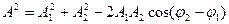- теорема косинусов.

Т. к. у = у₁ + у₂ и х = х₁ + х₂, то

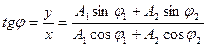
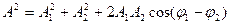
7.

Предположим, что колебания происходящие по закону 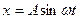происходят вдоль оси х. а колебания происходят по закону 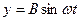по оси у.

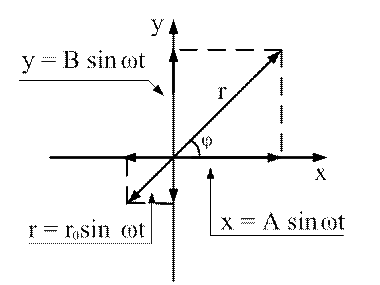
а). Фазы и частоты одинаковы, амплитуды различны.

Разделим почленно приведенные уравнения:

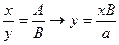(11)

Найдем r, то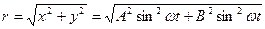

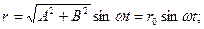
В результате сложения получается гармонические колебания с той же фазой и частотой происходящей вдоль линии отклоненной от оси х и на угол .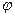

б). Колебания, отличающиеся на 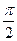, т.е.

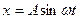(12)

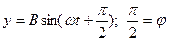
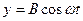(13)

Возведем уравнения (12) и (13) в квадрат, получим:

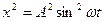(14)

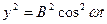(15)

Разделим уравнения (14) на(:А²), а уравнение (15) на (:В²)

,

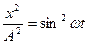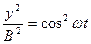
Сложим почленно последние два уравнения:

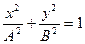. В результате сложения получилось уравнение эллипса. Полуосями эллипса являются А и В. в случае равенств амплитуд А и В получаем окружность.

8.

Свободными или затухающими колебаниями называется колебания, энергия которых ослабевает или уменьшается вследствие потерь, что приводит к уменьшению амплитуды колебания и к его затуханию. Пусть тело массой m колеблется вдоль оси х, под действием результирующей силы:

,

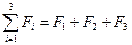где 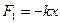- сила упругости.

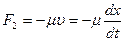- сила трения в зависимости от скорости движения, где 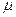- коэффициент трения.

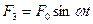- внешняя сила, изменяющаяся по синусоидальному закону.

В соответствии со вторым законом Ньютона уравнение колебательного движения можно записать.

, .

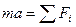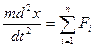а). Силы 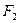и 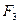равны нулю, в этом случае уравнение запишется 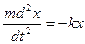, 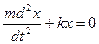- уравнение гармонического колебания происходящего под действием силы упругости.

Это движение происходящее в соответствии с этим уравнение описывается .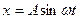

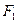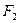б). Действуют силы и, а 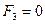- затухающие

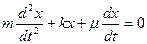(16)

Разделим обе части уравнения (6) на (m):

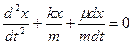(17) - уравнение гармонического колебания происходящего под действием силы трения и упругой силы.

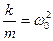- циклическая частота свободных затухающих колебаний протекающих в отсутствии .

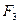Величена 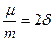, 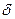- коэффициент затухания [1/c] и характеризует быстроту уменьшения амплитуды колебания.

С учетом последних формул мы получим 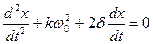- уравнение гармонически свободных колебаний.

Если на колеблющееся тело кроме силы упругости действует сила трения, то амплитуда колебаний будет уменьшаться и со временем колебания затухнут.

Изобразим изменение амплитуды свободного гармонического колебания графически.

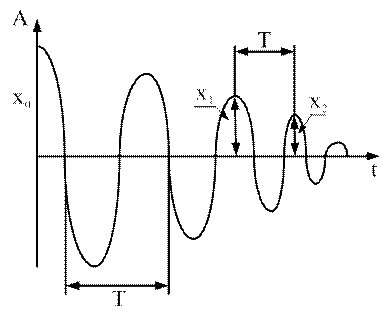
Амплитуда свободного гармонического колебания изменяются по закону: 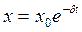- уравнение изменение амплитуды. Запишем это уравнение для х₁ и х₂:

.

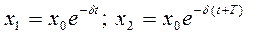Логарифм отношения 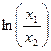называется логарифмическим декрементом затухания. 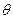- тетта, 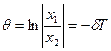- логарифмический декремент затухания, где 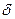- коэффициент затухания, - период.

в). Если к колеблющемуся телу приложена сила 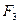, то тело будет совершать вынужденные колебания. Если частота соответственных колебаний тела совпадает с частотой действия внешней силы, то наступает явление резонанса, сопровождающееся резким увеличением амплитуды колебания.

9.

10.

Самостоятельно.

Дата добавления: 2014-01-03