Принцип работы однофазных трансформаторов

Принцип работы однофазных трансформаторов рассмотрим по схеме рис.10.2. При подключении источника напряжения 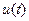в первичной обмотке трансформатора, возникает ток 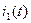. Далее будем пользоваться действующими значениями используемых физических величин.

Ток 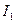приводит к появлению магнитодвижущей силы первичной обмотки

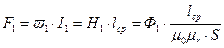. (10.1)

Магнитодвижущая сила 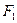возбуждает в магнитопроводе магнитный поток 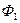причем

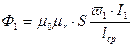. (10.2)

Магнитный поток 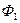индуцирует в первичной обмотке трансформатора ЭДС самоиндукции 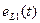, а во вторичной обмотке - ЭДС взаимной индукции .

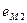Замкнем цепь вторичной обмотки. Под воздействием ЭДС взаимной индукции через нагрузку Z₂ потечет ток I₂ , возникает магнитодвижущая сила F₂, и магнитный поток Ф₂ , причем

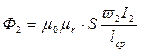. (10.3)

Для указанных на рис.10.2 направлений намотки обмоток трансформатора и выбранных положительных направлений токов I₁ и I₂ магнитные потоки Ф₁ и Ф₂ встречны. Поэтому в магнитопроводе создается результирующий магнитный поток

Рис. 10.2

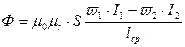. (10.4)

Этот поток пересекает витки обоих обмоток трансформатора и наводит в них результирующие ЭДС е₁ и е_2.

Помимо основного магнитного потока Ф (по 10.4), в реальном трансформаторе существуют потоки рассеяния первичной 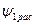и вторичной 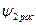обмоток. Для количественной оценки потоков 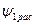и 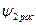вводят понятие эквивалентной индуктивности рассеяния так, что

; .

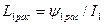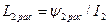Кроме того, обмотки реального трансформатора обладают активными сопротивлениями R₁ и R₂.

Чтобы учесть перечисленные величины при анализе работы трансформатора, переходят к его схеме замещения (рис.10.3).

Часть схемы, выделенная на рис. 10.3 пунктиром, не имеет активных сопротивлений и потоков рассеяния, а поэтому называется идеализированным трансформатором. К нему применимы все соотношения, полученные в лекции №8. Но для получения простых и наглядных соотношений параметров трансформатора необходимо преодолеть еще одну трудность.

Дело в том, что трансформатор в расчетном эквиваленте представляет собой нелинейную цепь. Значит, к его анализу, необходимо применять теорию нелинейной алгебры. Чтобы уйти от этого, гистерезисную зависимость 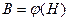заменяют эквивалентным эллипсом (рис.10.4), построенным так, что его площадь не менее чем на 95% перекрывает площадь петли гистерезиса.

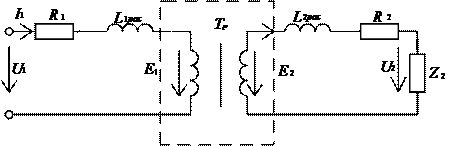Рис. 10.3

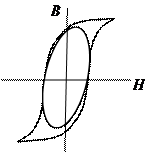
Рис. 10.4

Если теперь зависимости 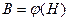, 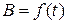; 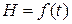выражать через параметры эллипса, то возникающие за счет отклонения от петли гистерезиса погрешности оказываются пренебрежимо малыми для практических целей. Главное в том, что применение эквивалентного эллипса позволяет перейти к простым линейным выражениям в представлении величин В (t) и Н (t):

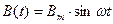; (10.5)

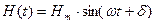, (10.6)

где 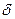- сдвиг фазы между Н и В.

От выражений (10.5) и (10.6) легко перейти к комплексной показательной форме представления, т.е.

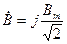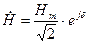; , (10.7)

Учитывая соотношения (8.14) и (8.15), связь между напряжением и магнитной индукцией представим в виде:

,

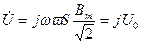а связь между током и напряженностью магнитного поля выражением:

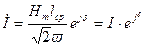. (10.8)

Теперь можно перейти к оценке основных параметров трансформатора. Учитывая (8.14) и (8.15) определяем напряжение на первичной и вторичной обмотках трансформатора:

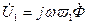, (10.9)

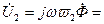
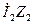. (10.10)

Эти напряжения полностью уравновешиваются ЭДС первичной 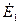и вторичной 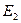обмоток:

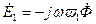, (10.11)

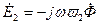. (10.12)

Отношение (10.10) к (10.9):

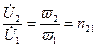(10.13)

называется коэффициентом трансформации.

Подставим в выражение для 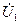значение Ф из (10.4):

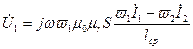. (10.14)

Если разомкнуть цепь вторичной обмотки, то ее ток I₂ станет равным нулю. При этом в цепи первичной обмотки будет протекать ток холостого хода, т.е. I₁ = I_1x, а выражение (10.14) примет вид

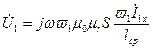. (10.15)

Но 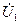- это напряжение источника. Оно не зависит от режима работы трансформатора. Значит левые части равенств (10.14) и (10.15) равны. Отсюда следует, что равны и правые части. Приравнивая их, определим ток холостого хода трансформатора.

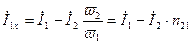. (10.16)

Последнее выражение показывает, что ток холостого хода равен разности токов первичной и вторичной обмоток, причем ток вторичной обмотки пересчитан к виткам первичной обмотки. Ток холостого хода мал и у мощных трансформаторов составляет единицы процентов от номинального значения.

Произведение 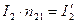называют приведенным током вторичной обмотки. Кроме 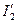для оценки качеств трансформатора пользуются приведенным сопротивлением нагрузки 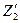и приведенным напряжением вторичной обмотки 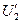. Определим их значения. Для этого выразим магнитный поток Ф из (10.10)

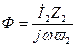. (10.17)

Подставим (10.17) в (10.9):

.

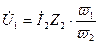Домножим и разделим последнее выражение на коэффициент 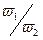. Перегруппировав множители, получим:

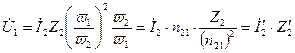. (10.18)

В (10.18) 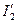- приведенный ток, а 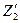- приведенное, т.е. пересчитанное к виткам первичной обмотки, сопротивление нагрузки.

Произведение

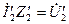(10.19)

называется приведенным напряжением вторичной обмотки. Очевидно, что

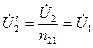. (10.20)

С учетом введенных понятий выражение (10.16) для тока холостого хода принимает вид:

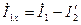. (10.21)

В выражении (10.15) множитель

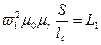
определяет индуктивность первичной обмотки. Поэтому можно записать:

,

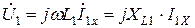что полностью соответствует закону Ома для цепи с индуктивностью.

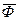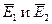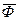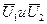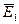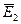Для завершения анализа принципа работы построим векторную диаграмму идеализированного трансформатора (рис.10.5). На диаграмме в качестве исходного принимаем вектор магнитного потока . Векторы ЭДС отстают от на 90⁰. Это очевидно из (10.11) и (10.12) по наличию множителя (-j). Векторы равны по величине и соответственно, но

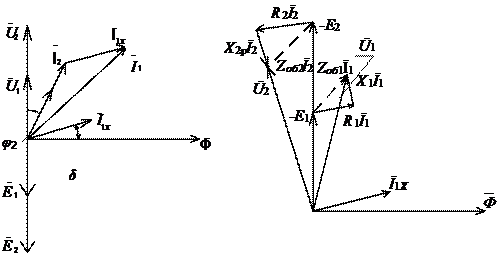Рис. 10.5 Рис. 10.6

противоположны им по направлению. Вектор тока холостого хода 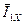опережает вектор 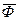на угол d. Это хорошо видно из (10.8) т.к.

.

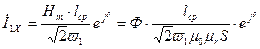Вектор тока вторичной обмотки трансформатора 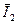сдвинут относительно вектора 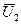на угол j ₂, что определяется характером нагрузки 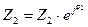. Значение вектора 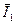легко найти по (10.21).

,

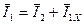что и выполнено на диаграмме.

Для перехода к реальному трансформатору обратимся к рис. 10.3. Схема рис. 10.3 содержит два электрически не связанных замкнутых контура - цепь первичной и цепь вторичной обмоток. Для каждой из них справедлив второй закон Кирхгофа. Поэтому для цепи первичной обмотки трансформатора справедливо равенство

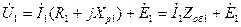. (10.22)

Равенство (10.21) показывает, что напряжение источника 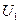уравновешивается падением напряжения на комплексном сопротивлении первичной обмотки и наводящейся в ней ЭДС самоиндукции 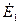. Эпюры напряжений, соответствующие (10.22) приведены на рис. 10.6.

Для цепи вторичной обмотки трансформатора можно записать равенство

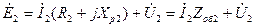. (10.23)

Эпюры напряжения, соответствующие (10.23) приведены на рис. 10.6.

Дата добавления: 2014-01-03