Равновесный и стационарный мембранные потенциалы. Потенциал покоя

Лекция 8.

Мембранные потенциалы и их ионная природа. Потенциал покоя. Уравнение Нернста. Уравнение Гольдмана-Ходжкина-Катца.

Механизм генерации потенциала действия. Распространение потенциала действия по миелиновым и безмиелиновым нервным волокнам.

Опыты Л. Гальвани и А. Вольта во второй половине XVIII в. привели к пониманию того, что функционирование живых тканей сопровождается электрическими явлениями. В настоящее время неоспоримым является тот факт, что генерация и распространение электрических потенциалов — это важнейшее физиче­ское явление в живых клетках и тканях.

Биопотенциалом называют разность электрических потенциалов, образующуюся между двумя точками клеток, тканей и орга­нов в процессе их жизнедеятельности. Биопотенциалы отражают функциональное состояние клеток и тканей. Поэтому их регистрация и анализ являются важным приемом при физиологических исследованиях и в диагностике.

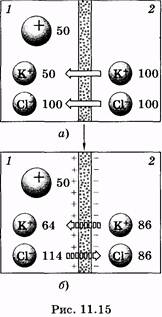Для понимания природы мембранных потенциалов — электри­ческих потенциалов, образующихся между внутренней и внешней сторонами мембраны, рассмотрим сначала модельную систему, представляющую собой сосуд, разделенный полупроницаемой мем­браной (рис. 11.15). Предположим, в левой части сосуда содержатся ионы калия, хлора и какие-либо крупные частицы, например молекулы белка, несущие положительный заряд (раствор 1). В правой части сосуда находятся только калий и хлор (раствор 2). Мембрана способна легко пропускать неорганические анионы и катионы, но является непроницаемой для молекул белка. Цифрами указаны относитель­ные концентрации соответствующих ионов, при которых разность потен­циалов составит около 10 мВ.

Общее число частиц в растворах одинаково (сохраняется их электронейтральность), однако концентрация ионов калия во втором растворе больше (см. рис. 11.15, а). Ионы калия устремятся из раствора 2 в рас­твор 1, а вслед за ними пойдут и ионы хлора (для сохранения электронейтральности растворов). При этом концентрация ионов хлора в пер­вом растворе еще больше возрастет. Этот процесс будет продолжаться до установления равновесного состояния (так называемого равновесия Доннана). Между двумя сторонами мембраны образуется разность потенциалов, которая уравновешивает кон­центрационный градиент ионов, способных к диффузии (на рис. 11.15, б потоки соответствующих ионов указаны штриховыми стрелками). Мембранная разность потенциалов рассчитывается по формуле Нернста:

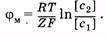(11.35)

Здесь с ₁ и с ₂ — молярные концентрации ионов по обе стороны мембраны, R — универсальная газовая постоянная, Т — термодинамическая температура, при которой происходит диффузия, F — постоянная Фарадея, Z — заряд иона. Эту разность потенциалов называют равновесным мембранным потенциалом. Мембранная теория происхождения биопотенциалов была выдвинута в 1902 г. Б. Бернштейном. Действительно, в живой клетке концентрация ионов калия значительно больше, чем в межклеточной жидкости, и крупные органические молекулы практически не проникают через мембрану. Важным доводом в пользу представлений Бернштейна послужил тот факт, что рассчитанная по формуле Нернста разность потенциалов между наружной и внутрен­ней сторонами мембраны мышечного волокна оказалась близкой к измеренной в опытах с помощью внутриклеточного микроэлектрода.

Однако «калиевая теория» мембранного потенциала оказалась несовершенной, не способной объяснить наблюдаемые впоследствии факты отклонения истинных значений потенциалов на мембранах живых клеток от теоретически рассчитанных. Оказалось, что равновесный мембранный потенциал характерен лишь для мертвых клеток, либо клеток с ослабленным метаболизмом.

В настоящее время общепризнанной теорией, объясняющей возникновение и поддержание потенциала на клеточной мембране в состоянии физиологического покоя, является теория А. Ходжкина. Она была развита и экспериментально обоснована им в 50-х гг. XX в. Сущность ее заключается в том, что потенциал, существующий на мембранах невозбужденных клеток (потенциал покоя), обусловлен полупроницаемыми свойствами клеточной мембраны и неравномерным распределением ионов между клеткой и окружающей средой. Это распределение поддерживается механизмами активного переноса, локализованными в самой мембране.

При получении выражения для потенциала покоя важно учитывать знаки ионов, проникающих через мембрану. Это можно сделать, в частности, обозначая знаком плюс плотности потоков положительных ионов и знаком минус — отрицательных. Основной вклад в создание и поддержание потенциала покоя вносят ионы натрия, калия и хлора. Суммарная плотность потока этих ионов с учетом их знаков равна

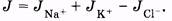(11.36)

Для живой клетки характерно не равновесное распределение веществ, но существование потоков ионов в обе стороны через мембрану. Такое состояние, при котором число различных ионов, проходящих в единицу времени через мембрану внутрь клетки, равно числу выходящих из клетки ионов, называют стационарным. Ясно, что в стационарном состоянии суммарная плотность потока ионов через мембрану равна нулю: J = 0.

Для плотности потоков положительных ионов натрия и калия и отрицательных ионов хлора запишем общее выражение на основании (11.33) и (11.34)

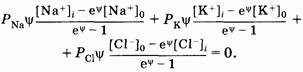(11.37)

Здесь квадратными скобками [ ] _i, и [ ]₀ обозначены концентрации ионов соответственно внутри и вне клетки. Сократив (11.37) на 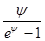, раскрыв выражения и перегруппировав их, получаем

P_Na[Na+] _i + Р_К[К+] _i + Р_Сl[Сl^-]₀ = e^y {P_Na[Na⁺]₀ + Р_К[К⁺]₀ + Р_С1[Сl^-] _i },

или

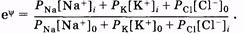
Логарифмируя это выражение, находим

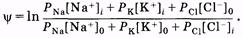(11.38)

Если от безразмерного потенциала вернуться к электрическому потенциалу [см. (11.29)], то из (11.38) получаем

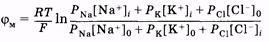(11.39)

Дата добавления: 2014-01-03