Уравнение Бернулли

Рассмотрим трубку тока малого сечения (рис. 1). Жидкость, выделенного объема, переместится из положении 1 в положение 2. Так как течение стационарное, то никаких энергетических изменений с жидкостью не произойдёт. Изменение энергии (потенциальной и кинетической) жидкости при перемещении объёма от положения 1 к 2 равно работе, которую необходимо совершить над жидкостью для перемещения выделенного объёма из положения 1 в положение 2. Считая объёмы цилиндрическими, можно записать:

V=S₁l₁=S₂l₂ (2)

Если скорость жидкости в пределах каждого заштрихованного объёма одинакова (равна v₁ и v₂ для положений 1 и 2 соответственно), то изменение кинетической энергии жидкости равно:

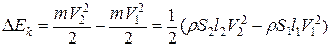, (3)

так как m=rS₁l₁=rS₂l₂, где r - плотность жидкости.

Вычислим работу внешних сил, действующих на жидкость. Силы со стороны соседних трубок тока нормальны к поверхности рассматриваемой трубки и работы не совершают. Работа сил, оказывающих давления р₁ и р₂ на торцы объёма 1 - 2 при его перемещении,

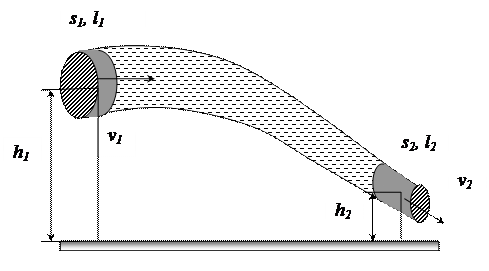Рис. 1. Схема трубки тока жидкости для вывода формулы Бернулли.

A_Р = F₁ l₁ - F₂ l₂ = p₁S₁ l₁ - p₂S₂ l₂. (4)

Работа силы тяжести:

А_Т = mgh₁ - mgh₂ = rS₁ l₁gh₁ - rS₂ l₂gh₂. (5)

Согласно закону сохранения энергии

DE_k= A_Р+ А_Т,

(rS₂l₂V₂² - rS₁l₁V₁²) = p₁S₁l₁ - p₂S₂l₂ + rS₁l₁gh₁ - rS₂l₂gh₂ (6)

откуда сокращая на S₁l₁ = S₂l₂ и перегруппировывая слагаемые, имеем:

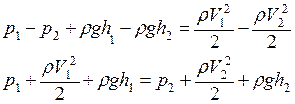
Так как выбор сечения трубки произволен, то индексы можно опустить:

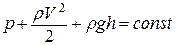. (7)

- это уравнение Бернулли.

Слагаемые, входящие в уравнение Бернулли имеют размерность и смысл давления. Давление р называют статическим; оно не связано с движением жидкости и может быть измерено, например, манометром, перемещающимся вместе с жидкостью.

Давление 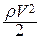называют динамическим; оно обусловлено движением жидкости и проявляется при ее торможении. Сумма статического и динамического давлений есть полное давление:

р_П = р + .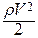

Давление rgh - весовое. В состоянии невесомости весовое давление отсутствует, с увеличением перегрузок оно возрастает.

В различных точках линии тока идеальной жидкости сумма статического, динамического и весового давлений одинакова.

Рассмотрим некоторые частные случаи, вытекающие из уравнения Бернулли.

1)Наклонная трубка тока постоянного сечения.

V = const, тогда p₁ + rgh₁ = p₂ + rh₂g или p₂ - p₁ = rg(h₁ - h₂),

Dp = rgDh.

В этом случае, как и в гидростатистике, разность давлений обусловлена разностью весов соответствующих столбов жидкости.

2)Горизонтальная трубка тока переменного сечения.

Всасывающее действие струи.

Так как h₁ = h₂ (рис. 2), то

.

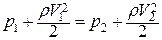Полное давление в разных сечениях горизонтальной трубки тока одинаково. В более узких местах S₂ < S₁, V₂ > V₁, p₂ < p₁.

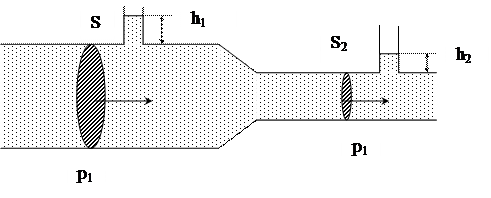Рис. 2.

Можно сделать столь узкое сечение трубки, что вследствие малого давления (ниже атмосферного) в это сечение будет засасываться воздух или жидкость (так называемое всасывающее действие струи). Это явление используют в водоструйных насосах, ингаляторах и пульверизаторах.

3) Измерение скорости жидкости. Трубка Пито.

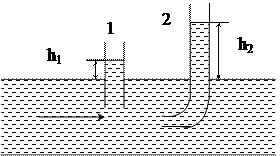Выберем в движущемся потоке жидкости точки 1 и 2, лежащие на одной линии тока (рис. 3).

Рис. 3

Так как трубка горизонтальная, а V₂ = 0, то на основании (7) запишем:

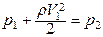, откуда .

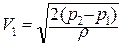Трубку 2, изображенную на рисунке называют трубкой Пито, по высоте h₂ столба жидкости в которой измеряют полное давление р₂.

Статическое давление р₁ движущейся жидкости определяют при помощи трубки 1 по высоте h₁ столба.

4) Закупорка артерии.

Образование атеросклеротической бляшки в артерии диаметром d₁ вызывает сужение просвета артерии до диаметра d₂ (рис.4).

Пусть артерия расположена горизонтально.

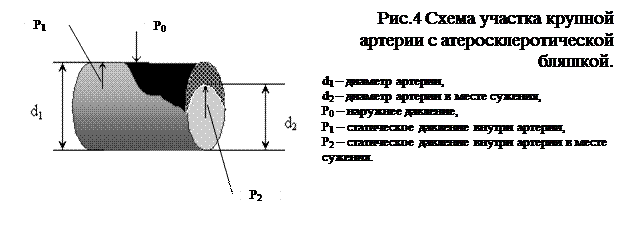
Течение крови по артерии будет происходить до того момента, пока статическое давление Р₂ в месте образования атеросклеротической бляшки будет превышать наружное давление на сосуд Р₀ (его можно считать приблизительно равным атмосферному). То есть, кровоток возможен при условии:

Р₂ - Р₀ ³ 0. (8)

Это реализуется, если d₂ ³ d_min.

Запишем уравнение Бернулли и условие неразрывности струи для нашего случая:

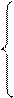
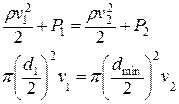(9)

Откуда 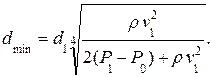(10)

Для сонной артерии: (нормальные условия)

средний диаметр d1 = 1 cм, скорость крови v1 = 0,2 м/с, плотность крови r = 1,05 × 10^3 кг/м^3, разница давлений Р1 - Р0 = 100 мм.рт.ст. = 1,33 × 10^4 Па

Вычисленный по формуле 10 минимальный диаметр сонной артерии равен d_min» 2 мм.

Если диаметр сужения станет меньше d_min, тогда под действием внешнего давления Р₀ просвет сосуда в месте расположения атеросклеротической бляшки закроется и кровоток полностью остановится. Однако, в организме как в любой сложной системе существуют компенсационные механизмы. При сужении артерии сердце начинает работать в более напряженном режиме, в результате чего давление Р₁ в артерии начнет возрастать, и кровь с усилием протекает через сужение. С помощью фонендоскопа можно услышать прерывистый шум во время работы сердца, свидетельствующий о нарушении нормального кровотока.

5) Разрыв аневризмы.

При некоторых патологиях наблюдается локальное снижение прочности и упругости кровеносных сосудов. Как следствие этого на некотором участке кровеносного сосуда его деформация под действием пульсирующего кровотока становится необратимой, и возникает вздутие сосуда (аневризма).

Скорость кровотока в месте развития аневризмы по условию неразрывности струи будет меньше, чем скорость кровотока в его недеформированной части. Согласно уравнению Бернулли, статическое давление в месте вздутия будет больше статического давления на участках сосуда нормального сечения. Нагрузка на расширенную часть сосуда увеличится, и возникшая аневризма под действием повышенного давления будет иметь тенденцию к расширению. В результате возможен разрыв аневризмы.

Вопрос 3. 14 минут.

Дата добавления: 2014-01-03