Течение вязкой жидкости. Формула Пуазейля

Ньютоновские и неньютоновские жидкости.

У большинства жидкостей (вода, низкомолекулярные органические соединения, истинные растворы, расплавленные металлы и их соли) коэффициент вязкости зависит только от природы жидкости и температуры. Такие жидкости называются ньютоновскими и силы внутреннего трения, возникающие в них, подчиняются закону Ньютона (формула 11).

У некоторых жидкостей, преимущественно высокомолекулярных (например, растворы полимеров) или представляющих дисперсионные системы (суспензии и эмульсии), h зависит также от режима течения - давления и градиента скорости. При их увеличении вязкость жидкости уменьшается вследствие нарушения внутренней структуры потока жидкости. Их вязкость характеризуют так называемым условным коэффициентом вязкости, который относится к определенным условиям течения жидкости (давление, скорость). Такие жидкости называются структурно вязкими или неньютоновскими.

Вопрос 4. 14 минут.

Занимаясь исследованием кровообращения, французский врач и физик Пуазейль пришел к необходимости количественного описания процессов течения вязкой жидкости вообще. Установленные им для этого случая закономерности имеют важное значение для понимания сущности гемодинамических явлений и их количественного описания.

Пуазейль установил, что вязкость жидкости может быть определена по объему жидкости, протекающей через капиллярную трубку. Этот метод применим только к случаю ламинарного течения жидкости.

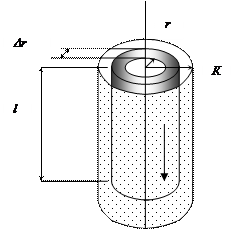
Пусть на концах вертикальной капиллярной трубки длиной l и радиусом R создана постоянная разность давлений Dр. Выделим внутри капилляра столбик жидкости радиусом r и высотой h. На боковую поверхность этого столбика действует сила внутреннего трения:

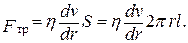(17)

		Рис. 6 Схема для вывода формулы Пуазейля.

Если р₁ и р₂ – давления на верхнее и нижнее сечения соответственно, то силы давления на эти сечения будут равны:

F₁=p₁pr² и F₂=p₂pr².

Сила тяжести равна F_тяж=mgh=rpr²gl.

При установившемся движении жидкости, согласно второму закону Ньютона:

F_тр+F_{давления}+F_тяж=0,

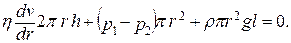
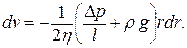Учитывая, что (р₁-р₂) = Dр, dv равно:

Интегрируем:

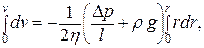
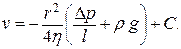
Постоянную интегрирования находим из условия, что при r=R скорость v=0 (слои, прилегающие непосредственно к трубе, неподвижны):

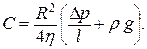
Скорость частиц жидкости в зависимости от расстояния от оси равна:

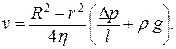
Объем жидкости, протекающий через некоторое сечение трубки в пространстве между цилиндрическими поверхностями радиусами r и r+dr за время t, определяется по формуле dV=2prdrvt или:

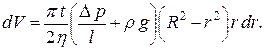
Полный объем жидкости, протекающей через сечение капилляра за время t:

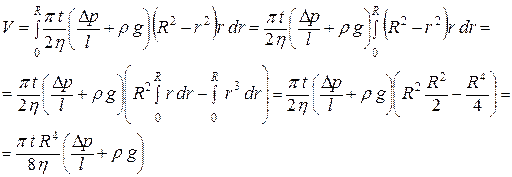
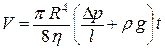(19)

В случае, когда пренебрегаем силой тяжести жидкости (горизонтальный капилляр), объем жидкости, протекающий через сечение капилляра, выражается формулой Пуазейля:

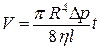(20)

Формулу 20 можно преобразовать: разделим обе части этого выражения на время истечения t. Слева получим объемную скорость течения жидкости Q (объем жидкости, протекающий через сечение за единицу времени). Величину 8hl/ 8pR⁴ обозначим через Х.. Тогда формула 20 принимает вид:

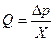(21)

Такая запись формулы Пуазейля (ее еще называют уравнением Гагена-Пуазейля) аналогична закону Ома для участка электрической цепи.

Можно провести аналогию между законами гидродинамики и законами протекания электрического тока по электрическим цепям. Объемная скорость течения жидкости Q является гидродинамическим аналогом силы электрического тока I. Гидродинамическим аналогом разности потенциалов j₁-j ₂ является перепад давлений Р₁ - Р₂. Закон Ома I = (j₁-j₂)/R имеет своим гидродинамическим аналогом формулу 20. Величина Х представляет собой гидравлическое сопротивление - аналог электрического сопротивления R.

Вопрос 5. 14 минут.

Дата добавления: 2014-01-03