
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Методы оценки параметров кривой обеспеченности годового стока при наличии, недостатке и отсутствии данных. Оценка точности определения параметров
|
|
|
|
Лекция № 9.
Методы оценки параметров кривой обеспеченности годовых величин стока при наличии гидрометрических рядов наблюдений.
При определении ординат аналитической кривой обеспеченности и расчетных значений гидрологических характеристик, так же как и при вычислении нормы годового стока, возможны три характерных расчетных случая: материалов многолетних гидрометрических наблюдений достаточно, недостаточно и совсем нет.
Многолетних гидрометрических рядов наблюдений достаточно. Параметры аналитической кривой обеспеченности, необходимые для определения ее ординат и построения, рекомендуется устанавливать методом наибольшого правдоподобия, методом моментов или графоаналитическим методом.
Метод наибольшого правдоподобия предложен английским математиком Р.Фишером. Он заключается в том, что параметры распределения подбирают по принципу наибольшого правдоподобия, т.е. принимают такие значения, при которых результаты наблюдений имеют наибольшую вероятность совместного появления, или, другими словами, наиболее правдоподобны.
Аналитическое решение этой задачи, данное С.Н.Крицким и М.Ф. Менкелем, требует громоздких вычислений. Поэтому с целью облегчения практического применения этого метода для трехпараметрического гамма-распределения Е.Г.Блохинов построил номограммы, которые позволяют определять расчетные значения коэффициента вариации Сv и коэффициента асимметрии Cs в зависимости от статистик 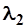 и
и 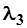 , вычисляемых по формулам:
, вычисляемых по формулам:
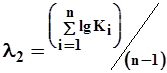
| (1) |
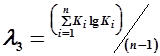
| (2) |
где Ki - модульный коэффициент рассматриваемой гидрологической характеристики; n - число членов рядов.
Среднемноголетнее значение гидрологических характеристик находят по формулам вида:
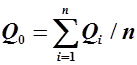
|
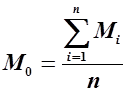
|
Метод моментов заключается в том, что параметры кривой обеспеченности (и распределения) устанавливают на основе понятия о моментах статистических совокупностей. По аналогии с механикой под моментами статистических совокупностей понимают произведения случайной величины x или ординаты кривой распределения на расстояние до выбранной точки. В математической статистике наиболее часто используют моменты двух видов; начальные - относительно начала координат и центральные - относительно среднего арифметического.
Начальный момент порядка m случайной величины x представляют собой выражение вида
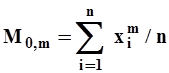
| (3) |
В частном случае при m=1 начальный момент, называемый первым, соответствует среднеарифметическому значению рассматриваемой переменной, т.е.
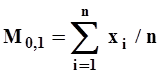
| (4) |
Это одна из формул метода моментов, позволяющая определить один из основных параметров аналитической кривой обеспеченности - норму стока.
Центральным моментом порядка m случайной величины x называют среднее значение отклонений x от ее среднеарифметического значения в степени m:
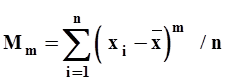
| (5) |
Второй центральный момент (при m=2)
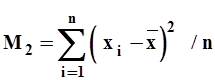
| (6) |
Если сопоставить это выражение с формулой
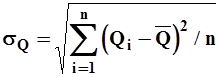
| (7) |
то окажется, что
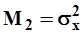
| (8) |
т.е. равен среднеквадратическому отклонению во второй степени (дисперсии). Откуда следует, что
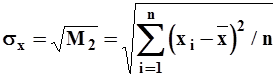
| (9) |
а коэффициент вариации
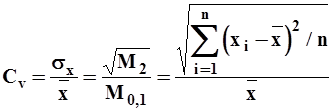 , ,
| (10) |
или в безразмерном виде
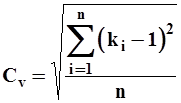
| (11) |
Третий центральный момент
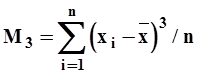
| (12) |
Откуда следует, что коэффициент асимметрии
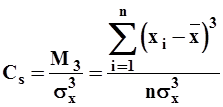
| (13) |
а для ряда модульных коэффициентов
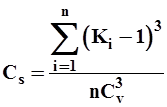
| (14) |
При наличии ограниченных выборок, второй центральный момент (8) имеет отрицательное смещение (систематическое занижение). Для его устранения в (8) вводится поправка 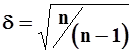 , c учетом этого получаем общее выражение
, c учетом этого получаем общее выражение
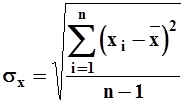
| (15) |
Соответственно этому и коэффициент вариации (10) примет следующий окончательный вид:
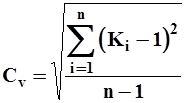
| (16) |
Как 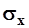 и
и 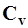 , параметр
, параметр 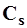 также является смешанной оценкой. Для устранения вводится поправка
также является смешанной оценкой. Для устранения вводится поправка 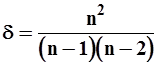 , тогда
, тогда
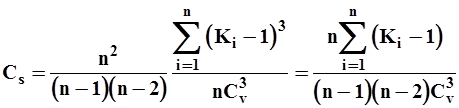
| (17) |
Графо-аналитический метод Г..А. Алексеева. Для определения параметров кривой обеспеченности, т.е. Q0, Cv, и Cs Г.А. Алексеева выполняем следуюшие процедуры:
1. Имеющийся ряд годовых расходов (объемов) Q1, Q2,,QN располагаем в убывающем порядке и получаем ранжированный ряд годовых расходов воды.
2. Используя формулы 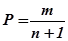 определяем величину обеспеченности для каждого члена ряда.
определяем величину обеспеченности для каждого члена ряда.
3. По парным значениям (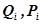 ) на клетчатке вероятностей строим сглаженную (осредненную) эмприческую кривую обеспеченности
) на клетчатке вероятностей строим сглаженную (осредненную) эмприческую кривую обеспеченности 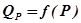 .
.
4. На кривой 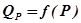 выбираем три опорные точки, соответствующие
выбираем три опорные точки, соответствующие  обеспеченности:
обеспеченности: 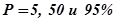 т. е.
т. е. 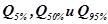 .
.
Вычисляем коэффициент скошенности
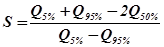 (18)
(18)
6. По значению 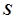 из пролежения 4 в книге «Практикум по инженерной гидрологии и регулированию стока. М: Колос, 1996. С.209-210» определяем параметры СS , Ф5%-Ф95%, Ф50%.
из пролежения 4 в книге «Практикум по инженерной гидрологии и регулированию стока. М: Колос, 1996. С.209-210» определяем параметры СS , Ф5%-Ф95%, Ф50%.
7. Определяем значения параметров кривой обеспеченности
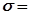
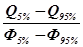 (19)
(19)
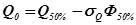 (20)
(20)
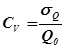 (21)
(21)
Данных гидрометрических наблюдений недостаточно. Параметры аналитической кривой обеспеченности устанавливают путем приведения коротких рядов к многолетнему периоду, используя многолетние наблюдения на реках-аналогах. Способы и условия такого приведения и расчета нормы годового стока при недостаточности данных наблюдений рассмотрены в лекций №7.
Если норма годового сток определяется непосредственно по уравнению регрессии
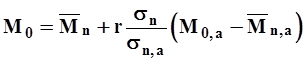
| (22) |
-первый способ, то коэффициент вариации вычисляют по формуле
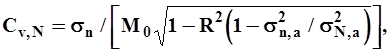
| (23) |
где 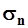 и
и 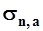 - среднеквадратические отклонения гидрологической характеристики за совместный период наблюдений соответственно для исследуемой реки и реки-аналога, л/(с·км2);
- среднеквадратические отклонения гидрологической характеристики за совместный период наблюдений соответственно для исследуемой реки и реки-аналога, л/(с·км2); 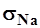 - то же за N-летний период для реки-аналога, л/(с·км2);
- то же за N-летний период для реки-аналога, л/(с·км2); 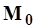 - норма годового стока, вычисляемая по уравнению регрессии для изучаемого створа, л/(с·км2); R - коэффициент корреляции между характеристиками стока в рассматриваемом пункте и пункте-аналоге.
- норма годового стока, вычисляемая по уравнению регрессии для изучаемого створа, л/(с·км2); R - коэффициент корреляции между характеристиками стока в рассматриваемом пункте и пункте-аналоге.
Если же уравнение регрессии (18) применяют для восстановления ежегодных значений стока - второй способ, а также при использовании графиков связи для удлинения рядов, параметры аналитической кривой обеспеченности рассчитывают так, как изложено выше, т.е. методами наибольшего правдоподобия и моментов или графоаналитическим методом.
Данные гидрометрических наблюдений отсутствуют. При отсутствии данных гидрометрических наблюдений норма стока и коэффициенты вариации определяют интерполяцией между значениями, полученными для рек-аналогов по данным наиболее продолжительных рядов гидрометрических наблюдений в рассматриваемом районе с учетом влияния местных факторов.
Коэффициент вариации, как и норму годового стока (см лекцию №7), допускается также определять по официальным картам этого параметра.
Оценка точности определения параметров. Мерой точности статистических параметров является средняя квадратическая погрешность (или стандарт погрешности).
При отсутствии внутрирядных связей стандартная погрешность среднего (Q0) определяется по формуле
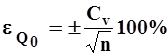
| (24) |
При наличии внутрирядных связей
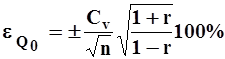
| (25) |
r - коэффициент корреляции между смежными членами; Cv - коэффициент вариации.
Стандартная погрешность коэффициента вариации Cv вычисленных методом моментов, находится по формуле
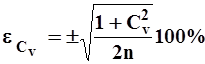
| (26) |
Если коэффициент вариации устанавливается с помощью метода наибольшего правдоподобия, то
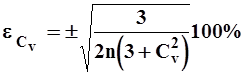
| (27) |
Относительная средняя квадратическая погрешность 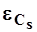 % коэффициента асимметрии по формуле С.Н.Крицкого и М.Ф.Менкеля
% коэффициента асимметрии по формуле С.Н.Крицкого и М.Ф.Менкеля
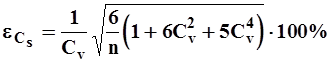
| (28) |
или же по следующей более простой эмпирической формуле
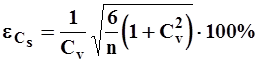
| (29) |
Влиянием связанности ряда в первом приближении можно в формулах (22)-(25) пренебречь.
Стандартная погрешность 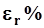 коэффициента корреляции r между смежными членами ряда
коэффициента корреляции r между смежными членами ряда
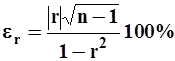
| (30) |
|
|
|
|
Дата добавления: 2014-01-03; Просмотров: 1203; Нарушение авторских прав?; Мы поможем в написании вашей работы!