Алгоритмы Лас Вегаса

Алгоритмы Лас Вегаса никогда не возвращают неправильный ответ, хотя иногда они не возвращают вообще никакого ответа. Чем дольше работают эти алгоритмы, тем выше вероятность того, что они вернут правильный ответ.

Алгоритм Лас Вегаса принимает случайное решение, а затем проверяет, приводит ли это решение к успеху. Программа, использующая алгоритм Лас Вегаса, вызывает его раз за разом, пока он не достигнет результата. Если обозначить через 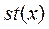и 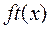время, необходимое для того, чтобы получить соответственно положительный или отрицательный ответ на входных данных длины 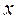, а через 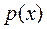- вероятность успешного завершения работы алгоритма, то мы приходим к равенству

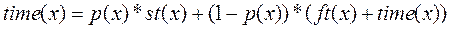
Это равенство означает, что в случае успеха затраченное время совпадает с временем получения успешного результата, а в случае неудачи затраченное время равно сумме времени на достижение неудачного результата и еще на один вызов функции. Решая это уравнение относительно 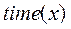, мы получаем

.

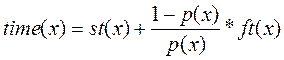Эта формула означает, что время выполнения зависит от времени получения успешного результата, безуспешного результата и вероятности каждого из этих исходов. Интересно, что при убывании вероятности р(х) успешного результата время выполнения все равно может быть невысоким, если скорость получения безуспешного результата возрастает. Поэтому эффективность можно повысить, если быстрее получать безуспешный результат. Как такой подход работает на практике?

Задача о расстановке ферзей.

Обратимся к задаче о расстановке восьми ферзей на шахматной доске так, чтобы они не били друг друга.

На рис. изображено одно из решений этой задачи. Рекурсивный алгоритм ее решения помещает ферзя в первой клетке первой вертикали, а затем вызывает себя для того, чтобы поставить ферзя на вторую горизонталь. Если в какой-то момент алгоритму не удается найти положения для очередного ферзя на очередной горизонтали, то алгоритм возвращается на предыдущий шаг и пробует другое размещение ферзя на предыдущей строке.

Имеется вероятностная альтернатива детерминированному рекурсивному алгоритму. Мы можем поочередно размещать ферзей на доске случайным образом на очередной свободной горизонтали доски. Отличие алгоритма Лас Вегаса от стандартного рекурсивного алгоритма состоит в том, что при невозможности разместить очередного ферзя алгоритм попросту сдается и сообщает о неудаче. Рекурсивный же алгоритм пытается добиться положительного результата.

Полный статистический анализ алгоритма показывает, что вероятность успеха равна 0.1293, а среднее число повторений, необходимых для его достижения, около 6.971. Приведенное выше уравнение показывает, что алгоритм выполнит при этом 55 проходов. Рекурсивному же алгоритму понадобится по крайней мере вдвое больше проходов.

Дата добавления: 2014-01-03