Лекция №8 пассивное резервирование с перераспределением нагрузки

Такое резервирование отличается тем, что система хоть и продолжает работать при отказе одного или нескольких элементов, однако оставшиеся исправные элементы будут работать в другом режиме. Надежность системы, резервированной с перераспределением нагрузки, повышается за счет того, что до отказа все элементы работают в облегченном режиме, а также, частично, за счет равномерного распределения нагрузки после отказа одного или нескольких элементов между оставшимися исправными.

Особенности расчета надежности рассмотрим на примере цепочки из двух резисторов (рис. 5.3), после включения которой в цепь нагрузка уменьшается вдвое (так как резисторы имеют одинаковый номинал R). Каждый резистор имеет интенсивность отказов λ₁. При обрыве (выходе из строя) одного из резисторов оставшийся резистор будет воспринимать полную (хотя и изменившуюся) нагрузку, и интенсивность его отказов, естественно, возрастет, то есть становится равной λ₂>λ₁.

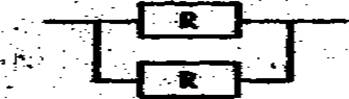
рис.5.3 Цепочка из двух резисторов

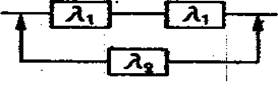
По отношению к внешней цепи интенсивность отказов одного из резисторов равна 2λ₁. Поэтому при расчете надежности цепочку (рис. 5.3) можно представить как систему с ненагруженным резервом, в которой основной элемент имеет интенсивность отказов, равную 2λ₁, а резервный элемент включается в работу после отказа основного и имеет интенсивность отказов λ₂ (рис. 5.4).

Рис.5.4 Включение резервного элемента в систему

Такая система будет работать безотказно на интервале времени (0,t) при следующих возможных событиях:

1) основной элемент не отказал на интервале времени (0, t);

2) основной элемент отказал в момент времени τ<t, сразу же включился резервный элемент и проработал безотказно в течение времени tτ.

Вероятность безотказной работы системы будет равна сумме вероятностей этих событий, то есть

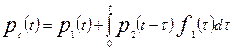(5.23)

где p₁(t) - вероятность безотказной работы основного элемента в течение времени t;

p₂(t—τ) — вероятность безотказной работы резервного элемента (после отказа основного элемента в течение времени (tτ);

f₁(τ)dτ= g₁(τ, τ+dτ) — вероятность отказа основного элемента на элементарном отрезке времени (τ, τ+dτ).

При показательном распределении вероятностей времени безотказной работы

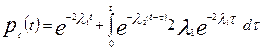(5.24)

После интегрирования по τ имеем

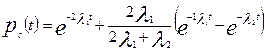(5.25)

Аналогичным образом можно рассчитать надежность для более сложных случаев пассивного резервирования. При расчете надежности цепочки из трех параллельно соединенных резисторов (при условии допустимого изменения сопротивления на 2/3 R) необходимо рассмотреть систему с двумя ненагруженными резервными элементами. При этом основной элемент имеет интенсивность отказов 3λ₁, первый резервный элемент -2λ₂, второй резервный элемент - λ₃, причем λз>λ₂>λ₁.

Прежде чем рассчитывать надежность систем при пассивном резервировании с перераспределением нагрузки, необходимо установить пределы изменения функциональных свойств системы в случае отказов ее основных n резервных элементов, так как эти пределы существенно влияют на ход расчетов.

Дата добавления: 2014-01-03