Основные этапы имитационного моделирования

Классификация имитационных моделей

Имитационные модели принято классифицировать по четырем наиболее распространенным признакам:

типу используемой ЭВМ;

способу взаимодействия с пользователем;

способу управления системным временем (механизму системного времени);

способу организации квазипараллелизма (схеме формализации моделируемой системы).

Первые два признака позволяют разделить имитационные модели на совершенно понятные (очевидные) классы.

По типу используемой ЭВМ различают аналоговые, цифровые и гибридные имитационные модели. Достоинства и недостатки моделей каждого класса общеизвестны. В дальнейшем будем рассматривать только цифровые модели.

По способу взаимодействия с пользователем имитационные модели могут быть автоматическими (не требующими вмешательства исследователя после определения режима моделирования и задания исходных данных) и интерактивными (предусматривающими диалог с пользователем в том или ином режиме в соответствии со сценарием моделирования). Моделирование сложных систем, относящихся, как уже отмечалось, к классу эргатических систем, как правило, требует применения диалоговых моделей.

Различают два механизма системного времени:

задание времени с помощью постоянных временных интервалов (шагов);

задание времени с помощью переменных временных интервалов (моделирование по особым состояниям).

При реализации первого механизма системное время сдвигается на один и тот же интервал (шаг моделирования) независимо от того, какие события должны наступать в системе. При этом наступление всех событий, имевших место на очередном шаге, относят к его окончанию.

Рис.2.1, а содержит иллюстрацию данного механизма. Так, для этого механизма считают, что событие 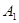наступило в момент окончания первого шага; событие 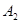- в момент окончания второго шага; события 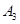, , 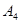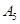- в момент окончания четвертого шага (эти моменты показаны стрелками) и т.д.

При моделировании по особым состояниям системное время каждый раз изменяется на величину, соответствующую интервалу времени до планируемого момента наступления следующего события, т.е. события обрабатываются поочередно - каждое «в свое время». Если в реальной системе какие-либо события наступают одновременно, это фиксируется в модели. Для реализации этого механизма требуется специальная процедура, в которой отслеживаются времена наступления всех событий и из них выделяется ближайшее по времени. Такую процедуру называют календарем событий.

На рис.2.1, б стрелками обозначены моменты изменения системного времени.

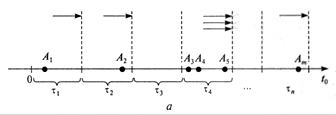
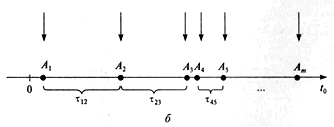
Рис.2.1. Реализация механизмов системного времени:

а) - с постоянным шагом; б) - с переменным шагом

Существует не столь распространенная разновидность механизма моделирования по особым состояниям, предусматривающая возможность изменения порядка обработки событий, так называемый механизм моделирования с реверсированием (обращением) шага по времени.

Согласно этому механизму, все события в системе разбиваются на два класса: фазовые и простые. К первым относят события, порядок моделирования которых нельзя изменять во избежание нарушения причинно-следственных связей в моделируемой системе. Остальные события относят к простым. Таким образом, сначала моделируют очередное фазовое событие, а затем все простые события до этого фазового, причем в произвольном порядке.

На рис.2.2 приведены перечисленные способы управления системным временем.

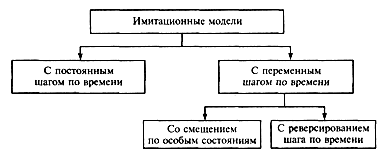
Рис.2.2. Механизмы управления системным временем

Очевидно, что механизм системного времени с постоянным шагом легко реализуем: достаточно менять временную координату на фиксированный шаг и проверять, какие события уже наступили.

Метод фиксированного шага целесообразно применять в следующих случаях:

события в системе появляются регулярно;

число событий велико;

все события являются для исследователя существенными (или заранее неизвестно, какие из них существенны).

Важнейшим классификационным признаком имитационных моделей является схема формализации моделируемой системы (способ организации квазипараллелизма).

Наибольшее распространение получили пять способов:

просмотр активностей;

составление расписания событий;

управление обслуживанием транзактов;

управление агрегатами; синхронизация процессов.

Характеристика этих способов требует введения ряда понятий.

Для задания свойств объектов используются атрибуты (параметры).

Совокупность объектов с одним и тем же набором атрибутов называют классом объектов. Все объекты делят на активные (представляющие в модели те объекты реальной системы, которые способны функционировать самостоятельно и выполнять некоторые действия над другими объектами) и пассивные (представляющие реальные объекты, самостоятельно в рамках данной модели не функционирующие).

Работа (активность) представляется в модели набором операторов, выполняемых в течение некоторого времени и приводящих к изменению состояний объектов системы. В рамках конкретной модели любая работа рассматривается как единый дискретный шаг (возможно, состоящий из других работ). Каждая работа характеризуется временем выполнения и потребляемыми ресурсами.

Событие представляет собой мгновенное изменение состояния некоторого объекта системы (т.е. изменение значений его атрибутов). Окончание любой активности в системе является событием, так как приводит к изменению состояния объекта (объектов), а также может служить инициатором другой работы в системе.

Под процессом понимают логически связанный набор активностей, относящихся к одному объекту. Выполнение таких активностей называют фазой процесса.

Различие между понятиями «активность» и «процесс» полностью определяется степенью детализации модели. Например, смена позиций мобильным объектом в одних моделях может рассматриваться как сложный процесс, а в других - как работа по изменению за некоторое время номера позиции.

Процессы, включающие одни и те же типы работ и событий, относят к одному классу. Таким образом, моделируемую систему можно представить соответствующим числом классов процессов. Между двумя последовательными фазами (работами) некоторого процесса может иметь место любое число фаз других процессов, а их чередование в модели, собственно, и выражает суть квазипараллелизма.

Способ просмотра активностей применяется при следующих условиях:

все ФД компонента реальной системы различны, причем для выполнения каждого из них требуется выполнение некоторых (своих) условий;

условия выполнимости известны исследователю заранее и могут быть заданы алгоритмически;

в результате ФД в системе наступают различные события;

связи между ФД отсутствуют, и они осуществляются независимо друг от друга.

В этом случае имитационная модель состоит из двух частей:

множества активностей (работ);

набора процедур проверки выполнимости условий инициализации активностей, т.е. возможности передачи управления на реализацию алгоритма этой активности.

Проверка выполнимости условия инициализации работы основана либо на анализе значений параметров и/или переменных модели, либо вычислении моментов времени, когда должно осуществляться данное ФД.

После выполнения каждой активности производится модификация системного времени для данного компонента и управление передается в специальный управляющий модуль, что и составляет суть имитации для этого способа организации квазипараллелизма.

Составление расписания событий применяется в тех случаях, когда реальные процессы характеризуются рядом достаточно строгих ограничений:

различные компоненты выполняют одни и те же ФД;

начало выполнения этих ФД определяются одними и теми же условиями, причем они известны исследователю и заданы алгоритмически;

в результате ФД происходят одинаковые события независимо друг от друга;

связи между ФД отсутствуют, а каждое ФД выполняется независимо.

В таких условиях имитационная модель, по сути, состоит из двух процедур:

проверки выполнимости событий;

обслуживания (обработки) событий.

Выполнение этих процедур синхронизируется в модельном времени так называемым списковым механизмом планирования.

Процедура проверки выполнимости событий схожа с ранее рассмотренными для просмотра активностей (напомним, что окончание любой работы является событием и может инициализировать другую активность) с учетом того, что при выполнении условия происходит не инициализация работы, а обслуживание (розыгрыш) события с последующим изменением системного времени для данного компонента.

Условия применимости транзактного способа организации квазипараллелизма были приведены при определении понятия «транзакт». Связь между приборами массового обслуживания устанавливается с помощью системы очередей, выбранных способов генерации, обслуживания и извлечения транзактов. Так организуется появление транзактов, управление их движением, нахождение в очереди, задержки в обслуживании, уход транзакта из системы и т.п. Событием в такой имитационной модели является момент инициализации любого транзакта.

Типовыми структурными элементами модели являются:

источники транзактов;

их поглотители;

блоки, имитирующие обслуживание заявок;

управляющий модуль.

Имитация функционирования реальной системы производится путем выявления очередной (ближайшей по времени) заявки, ее обслуживания, обработки итогов обслуживания (появления нового транзакта; поглощения заявки; изменения возможного времени поступления следующего транзакта и т.п.), изменения системного времени до момента наступления следующего события.

В случае построения имитационной модели с агрегатным способом организации квазипараллелизма особое внимание следует уделять оператору перехода системы из одного состояния в другое. Имитация производится за счет передачи управления от агрегата к агрегату при выполнении определенных условий, формирования различных сигналов и их доставки адресату, отработки внешних сигналов, изменения состояния агрегата и т.п. При этом в управляющем модуле осуществляется временная синхронизация состояний всех агрегатов.

Агрегатный способ прежде всего ориентирован на использование типовых математических схем (типовых агрегатов) для описания компонентов системы и организации их взаимодействия одним из перечисленных способов.

Процессный способ организации квазипараллелизма применяется в следующих случаях:

все ФД компонентов реальной системы различны;

условия инициализации ФД также различны;

в любой момент времени в данном компоненте может выполняться только одно ФД;

последовательность ФД в каждом компоненте определена.

Принято считать, что процессный подход объединяет лучшие черты других способов: краткость описания активностей и эффективность событийного представления имитации.

Процессным способом можно организовать имитацию АИС любой сложности, но такой способ особенно эффективен в тех случаях, когда требуется высокий уровень детализации выполнения 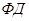, а сама имитационная модель используется для поиска «узких» мест в работе системы.

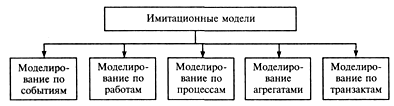
Рис.2.3. Классификация имитационных моделей по способу

организации квазипараллелизма

На рис.2.3 представлена классификация способов организации квазипараллелизма.

Отметим, что в настоящее время для реализации всех перечисленных схем формализации моделируемой системы созданы специализированные программные средства, ориентированные на данный способ организации квазипараллелизма, что, с одной стороны, облегчает программную реализацию модели, но, с другой стороны, повышает ответственность исследователя за правильность выбора соответствующей схемы.

Как уже отмечалось, имитационное моделирование применяют для исследования сложных экономических систем. Естественно, что и имитационные модели оказываются достаточно сложными как с точки зрения заложенного в них математического аппарата, так и в плане машинной реализации.

При этом сложность любой модели определяется двумя факторами:

сложностью исследуемого объекта-оригинала;

точностью, предъявляемой к результатам расчетов.

Использование машинного эксперимента как средства решения сложных прикладных проблем, несмотря на присущую каждой конкретной задаче специфику, имеет рад общих черт (этапов).

На рис.3.1 представлены этапы применения математической (имитационной) модели (по взглядам академика А.А.Самарского).

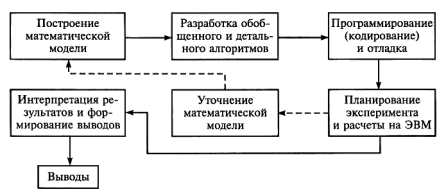
Рис.3.1. Этапы машинного эксперимента

Каждому из показанных на рисунке этапов присущи собственные приемы, методы, технологии.

После того как имитационная модель реализована на ЭВМ, исследователь должен выполнить последовательность следующих этапов (их часто называют технологическими):

испытание модели;

исследование свойств модели;

планирование имитационного эксперимента;

эксплуатация модели (проведение расчетов).

Кратко охарактеризуем первые два этапа (изложение методов математической теории планирования эксперимента и организации проведения модельных расчетов и обработки их результатов выходят за рамки настоящего учебника).

Испытание имитационной модели включает в себя следующее:

задание исходной информации;

верификацию имитационной модели;

проверку адекватности модели;

калибровку имитационной модели.

Задание исходной информации. Процедура задания исходной информации полностью определяется типом моделируемой системы:

если моделируется функционирующая (существующая) система, проводят измерение характеристик ее функционирования и затем используют эти данные в качестве исходных при моделировании;

если моделируется проектируемая система, проводят измерения на прототипах;

если прототипов нет, используют экспертные оценки параметров и переменных модели, формализующих характеристики реальной системы.

Верификация имитационной модели. Она состоит в доказательстве утверждений соответствия алгоритма ее функционирования цели моделирования путем формальных и неформальных исследований реализованной программы модели.

Неформальные исследования представляют собой ряд процедур, входящих в автономную и комплексную отладку.

Формальные методы включают:

использование специальных процессоров-«читателей» программ;

замену стохастических элементов модели детерминирован­ными;

тест на так называемую непрерывность моделирования и др.

Проверка адекватности модели. Количественную оценку адекватности модели объекту исследования проводят для случая, когда можно определить значения отклика системы в ходе натурных испытаний.

Наиболее распространены три способа проверки:

по средним значениям откликов модели и системы;

по дисперсиям отклонений откликов;

по максимальному значению абсолютных отклонений откликов.

Если возможность измерения отклика реальной системы отсутствует, оценку адекватности модели проводят на основе субъективного суждения соответствующего должностного лица о возможности использования результатов, полученных с использованием этой модели, при выполнении им служебных обязанностей (в частности, при обосновании решений - подробнее см.

Калибровка имитационной модели. К калибровке имитационной модели приступают в случае, когда модель оказывается неадекватной реальной системе. За счет калибровки иногда удается уменьшить неточности описания отдельных подсистем (элементов) реальной системы и тем самым повысить достоверность получаемых модельных результатов.

В модели при калибровке возможны изменения трех типов:

глобальные структурные изменения;

локальные структурные изменения;

изменение так называемых калибровочных параметров в результате реализации достаточно сложной итерационной процедуры, включающей многократное построение регрессионных зависимостей и статистическую оценку значимости улучшения модели на очередном шаге.

При необходимости проведения некоторых локальных и особенно глобальных структурных изменений приходится возвращаться к содержательному описанию моделируемой системы и искать дополнительную информацию о ней.

Исследование свойств имитационной модели. После испытаний имитационной модели переходят к изучению ее свойств.

При этом наиболее важны четыре процедуры:

оценка погрешности имитации;

определение длительности переходного режима в имитационной модели;

оценка устойчивости результатов имитации;

исследование чувствительности имитационной модели.

Оценка погрешности имитации, связанной с использованием в модели генераторов ПСЧ. Исследование качества генераторов ПСЧ проводится известными методами теории вероятностей и математической статистики. Важнейшим показателем качества любого генератора ПСЧ является период последовательности ПСЧ (при требуемых статистических свойствах). В большинстве случаев о качестве генератора ПСЧ судят по оценкам математических ожиданий и дисперсий отклонений компонент функции отклика. Как уже отмечалось, для подавляющего числа практических задач стандартные (встроенные) генераторы дают вполне пригодные последовательности ПСЧ.

Определение длительности переходного режима. Обычно имитационные модели применяются для изучения системы в типичных для нее и повторяющихся условиях. В большинстве стохастических моделей требуется некоторое время 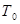для достижения моделью установившегося состояния.

Под статистическим равновесием или установившимся состоянием модели понимают такое состояние, в котором противодействующие влияния сбалансированы и компенсируют друг друга. Иными словами: модель находится в равновесии, если ее отклик не выходит за предельные значения.

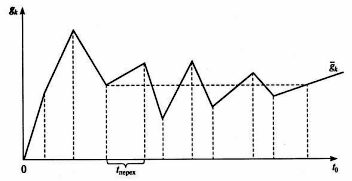
Рис.3.2. Определение длительности переходного периода

Существует три способа уменьшения влияния начального периода на динамику моделирования сложной системы:

использование «длинных прогонов», позволяющих получать результаты после заведомого выхода модели на установившийся режим;

исключение из рассмотрения начального периода прогона;

выбор таких начальных условий, которые ближе всего к типичным.

Для отделения переходного режима от стационарного у исследователя должна быть возможность наблюдения за моментом входа контролируемого параметра в стационарный режим. Часто используют такой метод: строят графики изменения контролируемого параметра в модельном времени и на нем выявляют переходный режим.

На рис.3.2 представлен график изменения 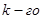контролируемого параметра модели 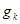в зависимости от модельного времени .

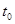На рисунке видно, что, начиная со времени 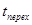этот параметр «вошел» в установившийся режим со средним значением .

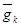Если построить подобные графики для всех (или большинства существенных) контролируемых параметров модели, определить для каждого из них длительность переходного режима и выбрать из них наибольшую, в большинстве случаев можно считать, что после этого времени все интересующие исследователя параметры находятся в установившемся режиме.

Оценка устойчивости результатов имитации. Под устойчивостью результатов имитации понимают степень их нечувствительности к изменению входных условий.

Универсальной процедуры оценки устойчивости нет. Практически часто находят дисперсию отклика модели 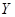по нескольким компонентам и проверяют, увеличивается ли она с ростом интервала моделирования. Если увеличения дисперсии отклика не наблюдается, результаты имитации считают устойчивыми.

Важная практическая рекомендация: чем ближе структура модели к структуре реальной системы и чем выше степень детализации учитываемых в модели факторов, тем шире область устойчивости (пригодности) результатов имитации.

Исследование чувствительности модели.

Работы на этом этапе имеют два направления:

установление диапазона изменения отклика модели при варьировании каждого параметра;

проверка зависимости отклика модели от изменения параметров внешней среды.

В зависимости от диапазона изменения откликов 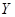при изменении каждой компоненты вектора параметров 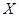определяется стратегия планирования экспериментов на модели.

Если при значительной амплитуде изменения некоторого компонента вектора параметров модели отклик меняется незначительно, то точность представления ее в модели не играет существенной роли.

Проверка зависимости отклика модели 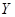от изменений параметров внешней среды основана на расчете соответствующих частных производных и их анализе.

Дата добавления: 2014-01-03