Функции на множестве натуральных чисел в комбинаторике

В школьном курсе изучается много функций, задаваемых на вещественной оси или ее подмножествах. Подмножества эти являются отрезками, интервалами, полуинтервалами,….. В настоящем параграфе мы определим те функции, которые можно рассматривать только на множестве N, и найдем их приложения в комбинаторике – разделе математики, посвященном решению задач выбора и расположения элементов конечных множеств.

Основой для всех таких функций можно считать факториал:

.

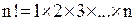1. Попробуем решить такую задачу: сколькими способами можно рассадить на n пронумерованных стульях n гостей? На первый стул можно посадить любого из n гостей. Выбрав одного из них, на второй стул можно усадить уже одного из оставшихся (n – 1) претендентов. Выбрав и этого, на третий стул выбираем одного из (n – 2) гостей…. На последний стул претендент будет только один. Таким образом, если двигаться от конца процесса, мы получим 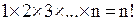вариантов.

Взаимно однозначное отображение конечного упорядоченного множества на себя называется подстановкой элементов множества. Каждая последовательность элементов конечного множества с учетом порядка называется перестановкой этих элементов и обозначается 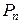. Перестановки не меняют элементов множества или их количества, они меняют порядок элементов. Таким образом, число всевозможных перестановок в множестве из n элементов 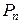= n!.

2. Представим теперь, что, как в предыдущей задаче, у нас n пронумерованных стульев, но мы рассаживаем на них m претендентов, причем m > n. Конечно, всех усадить мы не сможем, но хотим выяснить, сколько имеется вариантов рассаживания. Рассуждая так же, как в предыдущей задаче, видим, что на 1-й стул имеется m претендентов, на второй (m – 1), на третий (m – 2),…., на n-й стул остается (m – n + 1) претендент. Итак, число вариантов равно

.

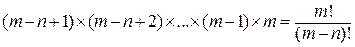Любой упорядоченный набор n различных элементов множества, состоящего из m элементов, называется размещением из m по n, число таких размещений обозначается 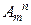. Таким образом,

=.

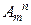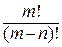3. Рассмотрим теперь несколько другую задачу, где мы «раздаем» не сидячие места на пронумерованных стульях (как известно, человек не может сидеть одновременно более, чем на одном стуле), а, например, n раритетных книг группе страстных библиофилов, состоящей из m человек. Сколько вариантов раздачи n книг m претендентам? На первую книгу у нас m претендентов, на вторую – тоже m претендентов, и так далее. Следовательно, мы имеем вариантов распределения книг между претендентами.

Любой упорядоченный набор n элементов множества, состоящего из m элементов, называется размещением с повторением из m по n и равен .

4. Вернемся ко второй задаче, где мы рассаживали m человек на n стульях, только теперь у нас стулья не пронумерованы, не отличаются друг от друга, и нас не интересует, где кто сидит, а интересует, сидит человек или стоит. Значит, число вариантов рассаживания совпадает с числом вариантов отбора из m гостей группы счастливчиков, состоящей из n человек, которые смогут сесть на стулья. Решение этой задачи можно связать с решением задачи 2. Представим, что мы решили бы задачу 2 таким образом: отбирали бы группы по n человек, а затем делали бы внутри группы отобранных для сидения n человек всевозможные перестановки, чтобы учесть все варианты рассаживания на пронумерованных стульях. Мы должны были бы получить тот же результат: 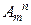. Следовательно, количество вариантов выбора групп по n человек из m человек равно 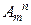, деленное на число перестановок в группе из n человек, то есть на .

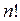Любое подмножество из n элементов множества, состоящего из m элементов, называется сочетанием из m по n, и число сочетаний обозначается 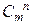. В соответствии с рассуждениями при решении задач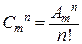и, или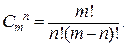

Дата добавления: 2014-01-03