Наискорейший спуск

В предыдущем методе поиск минимума предполагал поочередный спуск по координатам x и y. Однако можно спускаться по любому направлению, т.е. вдоль любой прямой линии r = r ₀ + at, где t — параметр, пробегающий значения от -¥ до +¥, а r, r ₀, a — векторы из некоторого конечномерного линейного пространства. В этом случае при спуске функция F (r ₀ + at) = f (t) зависит от одного аргумента — параметра t и ее минимум может быть найден, разобранными ранее методами.

Метод наискорейшего спуска получил название в связи с выбором специального направления спуска, а именно 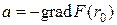. Как известно, локально градиент функции со знаком минус указывает на направление, в котором функция убывает наиболее быстро. Двигаясь по этому направлению, находим точку минимума r ₁ — новое приближения метода. В этой точке опять находим направление наискорейшего спуска, сдвигаемся по нему и так далее.

Рассмотрим частный случай, когда функция F является положительно определенной квадратичной функцией (матрица A = A^T > 0), т.е.

F (r) = (r, Ar) + (b, r) + c. (24)

Вдоль прямой r = r_n + at функция (24) имеет следующий вид:

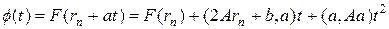. (25)

Согласно (25), функция f (t) является параболой, минимум которой 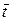легко находится

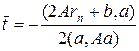, (26)

он дает возможность определить следующую точку спуска и значение функции F в этой точке:

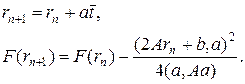(27)

Вычислим направление наискорейшего спуска для функции (24):

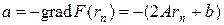. (28)

Подставляя (26), (28) в (27) получим окончательные уравнения для последующих шагов метода наискорейшего спуска.

Если рассматривать шаги метода наискорейшего спуска для функции (24) в базисе собственных векторов матрицы A, то можно вывести следующую оценку скорости сходимости

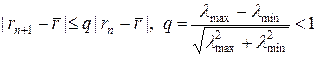, (29)

т.е. метод наискорейшего спуска сходится, причем линейно. В (29) 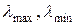— максимальное и минимальное собственные значения симметричной положительно определенной матрицы A.

Согласно (29), сходимость метода высока 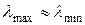при , при 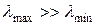показатель сходимости близок к единице, т.е. q» 1 и сходимость может оказаться крайне медленной. Геометрически последний случай отвечает крайне вытянутым эллипсам линий уровня.

На листинге_№6 приведен код программы, которая находит минимум методом наискорейшего спуска для функции (24). В программе матрица A конструируется из случайной матрицы, элементы которой распределены по нормальному закону со средним нуль и дисперсией один. В общем и целом для данного примера характерна довольно медленная сходимость метода наискорейшего спуска. Так при размерности линейного векторного пространства, равного n = 10 требуются тысячи итераций для удовлетворения довольно скромных запросов по точности сходимости (e = 10^-3).

Листинг_№6

%Программа моделирования метода наискорейшего

%спуска для поиска минимума положительно

%определенной квадратичной формы

%очищаем рабочее пространство

clear all

%задаем критерий остановки метода наискорейшего

%спуска: спуск прекращается, когда норма градиента

%функции F становится меньше заданного числа eps

eps=1e-3;

%определяем размерность линейного векторного

%пространства

n=12;

%определяем случайную матрицу

rnd=randn(n);

%определяем параметры квадратичной формы

A=rnd'*rnd; b=randn(1,n); c=randn;

%определяем формулу вычисления значения

%квадратичной формы и ее градиента

F=@(r)r'*A*r+b*r+c;

gradF=@(r)2*A*r+b';

%определяем начальный шаг наискорейшего спуска

rt=randn(n,1);

%задаем максимально допустимое число итераций

iterm=5000;

%определяем счетчик шагов и начальное значение

%нормы градиента

k=1; grF(k)=norm(gradF(rt));

%организуем цикл метода наискорейшего спуска

while (grF(k)>eps)&(k<iterm)

%вычисляем направление наискорейшего спуска

a=-gradF(rt);

%вычисляем значение параметра t, в которой

%квадратичная форма минимальна на данном шаге

tmin=-((2*A*rt+b')'*a)/(2*a'*A*a);

%находим новое положение спуска

rt=rt+a*tmin;

%увеличиваем значение счетчика и запоминаем

%значение нормы градиента на данном шаге

k=k+1; grF(k)=norm(gradF(rt));

end

%находим собственные значения матрицы A

lambda=eig(A);

lmax=max(lambda); lmin=min(lambda);

%оцениваем и выводим на печать показатель

%сходимости метода наискорейшего спуска

q=(lmax-lmin)/sqrt(lmax^2+lmin^2)

%рисуем график сходимости к нулю нормы градиента

%в зависимости от номера спуска

plot(1:k,grF);

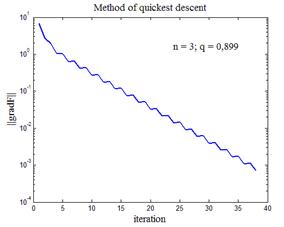
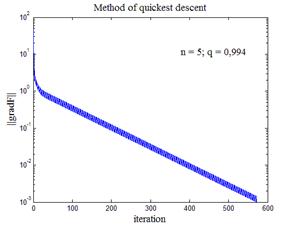
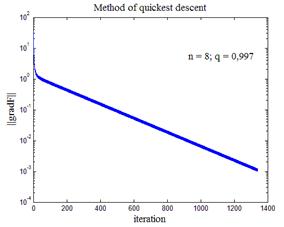
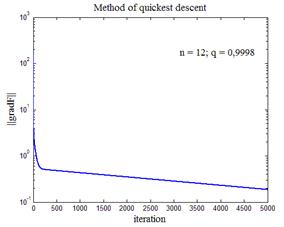
На рис.9 приведены некоторые варианты работы программы листинга_№6. Во всех четырех случаях строился график зависимости нормы градиента функции (24) от номера итерации. На каждом из четырех графиков приводится также размерность n пространства квадратичной формы (24), а также показатель q сходимости итераций в методе наискорейшего спуска, вычисленный согласно формуле (29). Из анализа графиков рис.9 видно, что, как правило, параметр q находится в окрестности единицы, поэтому сходимость крайне медленная. На рис.9,г не хватило и максимального количества итераций (5000) для выхода на заданную точность.

Рис.9,а. Траектория спуска нормы градиента к нулю (n = 3; q = 0,899)	Рис.9,б. Траектория спуска нормы градиента к нулю (n = 5; q = 0,994)
Рис.9,в. Траектория спуска нормы градиента к нулю (n = 8; q = 0,997)	Рис.9,г. Траектория спуска нормы градиента к нулю (n = 12; q = 0,9998)

Для улучшения сходимости метода наискорейшего спуска предлагают различного рода обобщения. Например, можно использовать следующее соображение. Пусть в направлении наискорейшего спуска делается бесконечно малый шаг, после чего вновь производится коррекция направления движения и т.д. В итоге производится движение по кривой r = r (t), которая является решением системы дифференциальных уравнений:

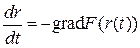. (30)

Учитывая (30), найдем

,

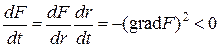т.е. функция F действительно уменьшается при движении по кривой r = r (t) и при t ® +¥ происходит приближение к минимуму.

Систему уравнений (30) можно истолковать как модель движения безынерционной точки вниз по градиенту.

Проиллюстрируем задачу (30) на примере поиска минимума потенциальной энергии небольшого кластера атомов, в котором функция потенциальной энергии описана на базе бинарного потенциала Леннарда-Джонса. Подобная задача уже рассматривалась в первой лекции применительно к моделированию плавления кристаллического образца.

Пусть r _i = (x_i, y_i, z_i), i = 1,…, n — положения в пространстве n атомов. Функция потенциальной энергии имеет следующий вид

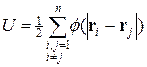, (31)

где

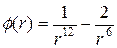. (32)

Подставляя (31), (32) в (30), находим

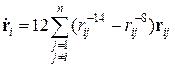, (33)

где r _ij = r _i - r _j, r_ij =| r _ij |. Коэффициент 12 в (33) можно отбросить и решать уравнения наискорейшего спуска в форме (30) как систему обыкновенных дифференциальных уравнений. Что и будет сделано в рамках кода программы, приведенного на листинге_№7.

Листинг_№7

%Программа поиска минимума функции потенциальной энергии

%кластера атомов на базе потенциала Леннарда-Джонса

function MinPotEnergy

%определим число атомов в кластере: 4^3=64

n=64;

%определим начальные положения атомов. Будем считать,

%что все атомы первоначально уложены в узлы

%кристаллической решетки с простой кубической

%симметрией.

for i=1:4

for j=1:4

for k=1:4

x(i+4*(j-1)+16*(k-1))=i-1;

y(i+4*(j-1)+16*(k-1))=j-1;

z(i+4*(j-1)+16*(k-1))=k-1;

end

end

end

%создаем рабочее окно и оси трехмерной системы координат

hF=figure('NumberTitle','off','Name',...

'Minimum of potential energy','Color',[0.8 0.8 0.8]);

hA=axes('Parent',hF,'Units','pixels',...

'Position',[95 50 350 350]);

axis([-0.5 3.5 -0.5 3.5 -0.5 3.5]);

%рисуем начальные положения атомов в кластере

hL=line(x,y,z,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

pause(0.5);

delete(hL);

%используем решатель системы жестких дифференциальных

%уравнений ode15s для решения системы уравнений (30)

u=[x y z];

[t r]=ode15s(@gradU,[0 300],u);

%формируем цикл изображения того, как атомы кластера

%стремятся к положениям, в которых реализуется минимум

%потенциальной энергии

k=0;

for i=1:5:length(t)

x=r(i,[1:n]); y=r(i,[(n+1):2*n]); z=r(i,[(2*n+1):3*n]);

hL=line(x,y,z,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

pause(0.5);

delete(hL);

u=[x y z];

k=k+1;

%запоминаем норму правой части системы

%дифференциальных уравнений

error(k)=norm(gradU(0,u));

end

hL=line(x,y,z,'Color','black',...

'LineStyle','none','Marker','.','MarkerSize',18);

%строим график нормы вектора правых частей системы

%дифференциальных уравнений. При выходе на минимум эта

%норма должна стремиться к нулю

plot(1:k,error);

%определяем функцию, которая возвращает правую часть

%системы диффернциальных уравнений

function f=gradU(t,u)

n3=length(u); n=n3/3;

x=u([1:n]); y=u([(n+1):2*n]); z=u([(2*n+1):3*n]);

for i=1:n

sx=0; sy=0; sz=0;

for j=1:n

if i~=j

rij2=(x(i)-x(j))^2+(y(i)-y(j))^2+(z(i)-z(j))^2;

sx=sx+(rij2^(-7)-rij2^(-4))*(x(i)-x(j));

sy=sy+(rij2^(-7)-rij2^(-4))*(y(i)-y(j));

sz=sz+(rij2^(-7)-rij2^(-4))*(z(i)-z(j));

end

end

ux(i)=sx; uy(i)=sy; uz(i)=sz;

end

f=[ux'; uy'; uz'];

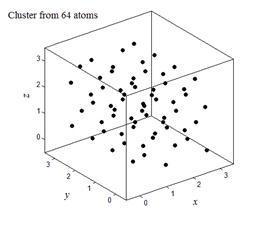
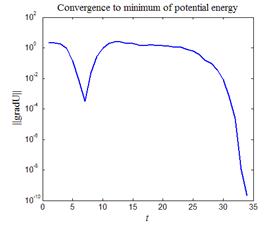
Итог работы кода программы листинга_№7 определяется парой графиков на рис.10. На рис.10,а приведено равновесное положение атомов кластера, т.е. такое положение атомов которое отвечает минимуму потенциальной энергии (31). На рис.10,б приведена динамика нормы вектора градиента функции потенциальной энергии, которая характеризует точность выхода в минимум потенциальной энергии. Положения атомов, отвечающие точному локальному минимуму потенциальной энергии, обращают норму градиента потенциальной энергии в нуль. Необходимо отметить, что в данной задаче функция потенциальной энергии допускает большое количество локальных минимумов. По некоторым оценкам число локальных минимумов 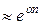(не считая n! перестановок атомов).

Рис.10,а. Положения атомов в кластере, обеспечивающие минимум потенциальной энергии	Рис.10,б. Зависимость нормы градиента функции потенциальной энергии от параметра t системы уравнений (30)

В условиях неупорядоченного рельефа все методы спуска не дают способ поиска глобального минимума, т.к. из данного начального приближения сходятся к одному-единственному локальному минимуму. В этих условиях применяют случайный поиск. В предыдущем примере находился минимум функции потенциальной энергии для кластера из 64 атомов, т.е. размерность пространства составляла 64´3 = 192. В этой ситуации использовать случайный поиск напрямую нереально по следующим соображениям. Пусть первый атом в кластере может принимать 10³ случайных позиций в ящике (в среднем по десять точек на каждую координату), представленном на рис.10,а. Все другие атомы кластера также независимо могут принимать 10³ случайных позиций. Всего, таким образом, получится 10¹⁹² начальных конфигураций для кластера в целом. Применяя метод спуска к каждой из этих начальных позиций, получим набор локальных минимумов. Сравнивая полученные локальные минимумы друг с другом, можем найти среди них тот, который имеет наименьшее значение, но даже эта процедура не гарантирует получение глобального минимума. Помимо этого цифра 10¹⁹² абсолютно немыслима, поэтому для поиска глобального минимума, если его вообще возможно найти, необходимо использовать ту или иную имеющуюся априорную информацию.

Дата добавления: 2014-01-03