Пример. Покажем, что существуют зависимые случайные величины, для которых

Покажем, что существуют зависимые случайные величины, для которых 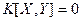. Пусть

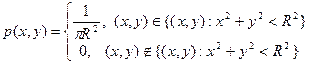
Тогда плотности распределения случайных величин 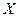и 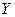равны соответственно

, .

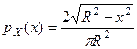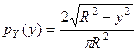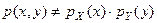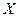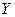Отсюда видно, что , т.е. и – зависимые случайные величины. Вычислим корреляционный момент этих случайных величин по формуле

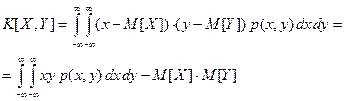
Найдем вначале математические ожидания случайных величин

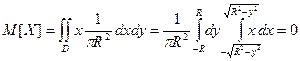
Здесь внутренний интеграл равен нулю как интеграл от нечетной функции по симметричному относительно 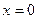промежутку.

Аналогично 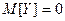. Следовательно,

.

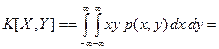
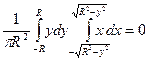Случайные величины называются некоррелированными, если их корреляционный момент равен нулю и коррелированными, если их корреляционный момент не равен нулю.

Если случайные величины 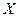и 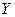независимы, то они некоррелированы.

Если случайные величины 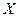и 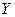зависимы, то они могут быть коррелироваными и некоррелироваными.

Если случайные величины 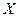и 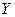некоррелированы, то они могут быть зависимыми и независимыми.

Если случайные величины 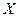и 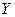коррелированы. то они зависимы.

Матрицей ковариаций 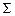случайных величин 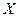и 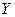называется симметричная квадратная матрица второго порядка, на главной диагонали которой расположены дисперсии случайных величин 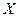и 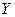, а на побочной диагонали – корреляционные моменты, т.е.

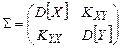. (21)

Дата добавления: 2014-01-03