Асимптоты кривой

Определение. Прямая называется асимптотой кривой, если расстояние 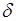от переменной точки M кривой до этой прямой при удалении точки M в бесконечность стремиться к нулю.

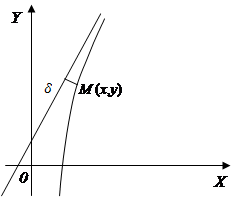Асимптоты бывают вертикальными, они показывают поведение функции в окрестности особой точки, когда 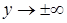, и наклонными, дающими представление о поведении функции при .

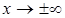Если 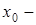особая точка, уравнение вертикальной асимптоты .

Теорема. Кривая 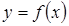имеет наклонную асимптоту при , уравнение которой , если принимают конечное значение и .

Доказательство. Из определения асимптоты следует , где бесконечно малая при , то есть . Остается определить параметры уравнения асимптоты. Для этого вычислим , 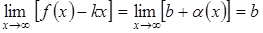. Итак, если оба предела существуют и конечны, параметры прямой и определены, причем точки этой прямой бесконечно сближаются с точками кривой при .

Пример. . Ясно, что - уравнение вертикальной асимптоты.

Определим ,

.

Наклонная асимптота при имеет уравнение .

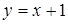Исследование функции, построение ее графика

Алгоритм исследования

I. Исследование самой функции. Необходимо установить

1) Область определения функции, ее особые точки, вертикальные асимптоты.

2) Точки пересечения кривой с осями координат

3) Функция четная, нечетная или общего вида

4) Функция периодическая или не периодическая

II. Исследование производной функции. Необходимо определить

1) Точки максимума и минимума функции

2) Интервалы возрастания и убывания функции

III. Исследование второй производной

1) Точки перегиба

2) Интервалы выпуклости и вогнутости функции

IV. Исследование поведения функции при . Наклонные асимптоты.

В качестве примера рассмотрим функцию

I.

1. Область существования функции – вся числовая ось, то есть . Следовательно, у этой кривой нет особых точек, нет и вертикальных асимптот.

2. Кривая пересекает оси координат в начале координат. Следовательно, первая характерная точка графика .

3. Кривая нечетная: 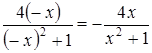, следовательно, она симметричная относительно начала координат.

4. Функция непериодическая.

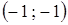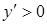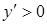II. 1. Определим первую производную , приравниваем ее нулю, откуда получаем еще две характерные (критические) точки , , координаты этих точек на плоскости , . Рассмотрим первую из этих точек , левее ее производная , правее , следовательно, это точка минимума функции. Левее точки производная правее она отрицательна, значит это точка максимума функции.

2. Знак первой производной определяется выражением 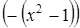, следовательно, она положительна на интервале , в остальных областях она отрицательна. Итак, функция убывает на интервале , возрастает на интервале , затем опять убывает на .

III. 1. Определяем вторую производную функции:

.

Приравниваем производную нулю и получаем еще три характерные точки функции, одна из которых уже известна. Две другие и . На координатной плоскости они имеют координаты , . Знак второй производной определяется ее числителем. Левее точки она отрицательна, правее . Следовательно, это точка перегиба. Левее точки имеем , правее ., еще одна точка перегиба. Левее точки получаем , правее , третья точка перегиба.

2. Поскольку других точек, в которых вторая производная меняет знак у функции нет, можно утверждать, что на интервале 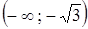кривая выпуклая, на интервале кривая вогнутая, на интервале кривая опять выпуклая и, наконец, на интервале - вогнутая.

IY. Определяем наклонные асимптоты кривой, уравнение асимптоты , причем

,

,

Поскольку уравнение асимптоты , асимптотой функции является ось .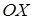

В итоге график функции имеет вид

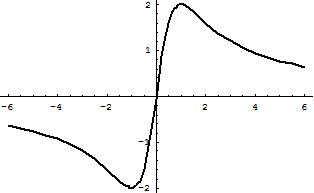
На рисунке отчетливо наблюдаются точки максимума и минимума функции и три точки перегиба. Видим также, что кривая «прижимается» к ос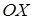и при , стремящемся как к плюс, так и к минус бесконечности, следовательно, асимптота единая.

Рассмотрим пример при другом оформлении результата. Пусть . Область существования данной функции – вся числовая ось, кроме точки . Функция непериодическая (нет тригонометрических функций), общего вида (не четная, не нечетная).

Определим вначале все характерные точки графика, то есть точки пересечения с осями координат, особые точки, точки максимума и минимума, точки перегиба. Для этого вычислим первую и вторую производные

,

.

Исследуя функцию и ее производные, устанавливаем, что имеется одна особая точка и еще три характерных точки , , .

Таблица

		-2		-1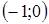
	<0	-8	<0	-9	<0		>0	н.с.	>0
	<0		<0		>0		>0	н.с.	<0
	<0		>0	>0	>0		>0	н.с.	>0
Примеч.	, убыв., выпукл.	Т. Пер.	, убыв., вогн.	Min	, возр., вогн.		, возр., вогн.	Н.с.	, убыв., вогн.

В таблице собрана вся информация о функции, примечания позволяют проще построить ее график.

Определим наклонную асимптоту кривой , причем

,

.

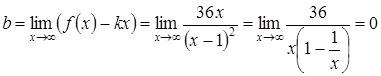Дата добавления: 2014-01-03