Подвижность ионов, закон Кольрауша

В бесконечно разбавленных растворах эквивалентная электро­проводность достигает предела и от концентрации больше не зависит, так как в растворах слабых электролитов наступает полная диссоциация (α = 1), а в растворах сильных электролитов межионное взаимодействие исчезает.

Эквивалентная электропроводность бесконечно разбавленных растворов называется электропроводностью при бесконечном разведении и обозначается l_∞ (или l₀).

Эквивалентная электропроводность при бесконечном разведении, согласно закону независимого движения ионов Кольрауша, равна сумме предельных подвижностей ионов

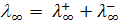(10.5)

Подвижность связана с абсолютной скоростью движения ионов n:

l⁺=n⁺ F, l^-=n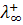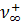^- F, 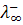=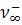F, =F

где F – число Фарадея, 96487 к. ≈ 96500к.

Под абсолютной скоростью движения иона v, понимают скорость перемещения его в электрическом поле с градиентом потенциала 1 в/см. Размерность n см² сек^-1 – в^-1. Величина абсолютной скорости движения иона при прочих равных условиях (температура, вязкость среды, градиент поля) зависит от концентрации раствора и достигает предельного значения в бесконечно разбавленных растворах, т. е. при φ→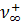∞, n ⁺→ , n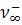^-→ .Taк как скорость движения ионов очень мала, то используют величины в F раз большие — подвижности l ⁺ и l ^-.

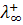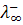Подвижность также называется эквивалентной электропроводностью ионов. Она измеряется в тех же единицах, что и эквивалентная электропроводность электролита (Ом^-1см²-г-экв^-1). Подвижности ионов зависят от концентрации, особенно в растворах сильных электролитов, в которых межионное взаимодействие велико (f_l < 1). Предельные подвижности ионов и достигаются при бесконечном разведении (φ→∞,f_l →1), их значения приводятся в справочной литературе.

Зависимость эквивалентной электропроводности от степени дис­социации и межионного взаимодействия описывается уравнением:

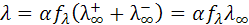(10.6)

В растворах слабых электролитов число ионов, участвующих в переносе электричества, определяется степенью диссоциации a. В концентрированных растворах слабых электролитов α весьма мала, поэтому и число ионов в растворе также мало и практически отсутствует межионное взаимодействие. При сильном разбавлении растворов α возрастает и увеличивается число
ионов в растворе, однако межионные расстояния так велики, что взаимодействие ионов также отсутствует (f_l = 1). Таким образом, в растворах слабых электролитов при любых разведениях ионы обладают предельной подвижностью 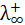и 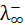и эквивалентная электропроводность зависит только от степени диссоциации

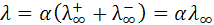
Следовательно, отношение электропроводностей будет отвечать степени диссоциации слабых электролитов

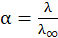(10.7)

Это уравнение называют формулой Аррениуса, на практике его используют для определения степени диссоциации растворов электролитов.

Для 1–1–валентного слабого электролита, диссоциирующего по схеме АВ↔А+ В^–, используя закон разведения Оствальда и учитывая, что 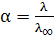можно определить константу диссоциации через эквивалентную электропроводность по формуле:

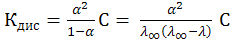(10.8)

где С – концентрация электролита, моль/л.

Согласно теории Дебая-Хюккеля, сильные электролиты в растворах полностью диссоциированы на ионы (α =1) и межионные взаимодействия велики (f_l < 1), значит уравнение (10.6) должно быть записано в виде

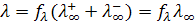(10.9)

откуда коэффициент электропроводности равен

;

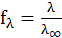Коэффициент электропроводности является функцией концентрации, экспериментально его определяют исходя из эквивалентной электропроводности раствора. Величина 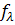зависит от валентности ионов: 1–1–валентного электролита (типа NaCI, HCI) в 0,1 н. растворе 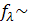0,8; для 1–2–валентных (Na₂SО₄, СаСI₂) f_x ~ 0,75; 2–2–валентных (CuSО₄) 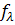~ 0,4. При разбавлении растворов уменьшается межионное взаимодействие, и эти различия сглаживаются: эквивалентная электропроводность достигает предела 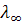и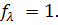

10.4 Механизм влияния ионов атмосферы на электропроводность
растворов, закон квадратного корня Кольрауша.

Качественно механизм влияния ионной атмосферы на электропроводность состоит в следующем: центральный ион, например катион, при наложении постоянного электрического поля движется к катоду, противоположно заряженная ионная атмосфера перемещается к аноду. Это вызывает так называемое электрофоретическое торможение.

Окружающая центральный ион атмосфера должна исчезать позади иона, движущегося в электрическом поле, и вновь образовываться впереди него. Оба процесса разрушения и образования ионной атмосферы происходят не мгновенно, например в 0,1 н растворе хлористого калия за 0,6·10^-9 сек, а в 0,001 н растворе – за 0,6·10^-7сек. Это вызывает релаксационное торможение. Поэтому коэффициент электропроводности принимает значения меньше единицы не в результате неполной диссоциации, а за счет проявления этих торможений.

Кроме электрофоретического и релаксационного торможения, существует третья сила, тормозящая движение ионов в растворе. Это сила трения, зависящая от вязкости растворителя, в котором движется ион. Поэтому повышение температуры вызывает увеличение скорости движения ионов, и как следствие возрастание электропроводности.

Для разбавленных растворов сильных электролитов теория дает линейную зависимость эквивалентной электропроводности от корня квадратного из концентрации (закон квадратного корня Кольрауша)

(10.9)

Постоянная А, зависящая от природы растворителя, температуры и валентного типа электролита, экспериментально определяется тангенсом угла наклона прямой 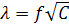к оси абсцисс (рис. 10.2).

Предельную эквивалентную электропроводность 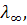сильных электролитов можно найти экстраполяцией опытных данных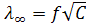до значения С = 0. Необходимо подчеркнуть, что, хотя предельную электропроводность понимают как проводимость при концентрации электролита, близкой к нулю, она никоим образом не идентична эквивалентной электропроводности растворителя.

Рис. 10.2 Зависимость эквивалентной электропроводности от корня квадратного из концентрации для сильных электролитов (НСI, КОН, LiCI) , и слабого электролита (СН₃СООН) в водных растворах.

Для растворов слабых электролитов зависимость эквивалентной
электропроводности от концентрации вытекает из закона разбавления Оствальда. При α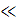1 получаем

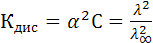(10.10)

откуда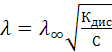

или в логарифмическом виде

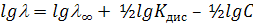
Эта зависимость не является линейной, поэтому значение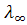, не­возможно определить экстраполяцией, его определяют только косвенным путем исходя из закона независимого движения ионов Кольрауша.

Данные о подвижности ионов показывают, что радиусы ионов в кристаллической решетке не сохраняются в растворах. Например, радиусы
ионов щелочных металлов по ряду Li⁺<Na⁺<K⁺<Rb⁺<Cs⁺ возрастают, однако в растворе наблюдается обратный порядок. Ион Li ⁺ имеет более сильное электрическое поле, так как его удельный заряд (отношение величины заряда частицы к ее массе) больше, чем других щелочных ионов, поэтому в растворе он гидратируется сильнее. Сильно гидратированный ион Li⁺ движется между молекулами воды в электрическом поле гораздо медленнее, чем менее гидратированпый ион Cs⁺ (например,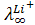= 38,6; 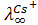= 77,2 ом^{-1 см 2} г-экв^-1).

С увеличением заряда ионов скорость перемещения его в элек­трическом поле, а, следовательно, и электропроводность раствора возрастают. Однако самыми большими скоростями обладают ионы Н+ (точнее ионы гидроксония) и ОН^-. Только их подвижности выражаются трехзначными числами (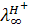= 349,8; =198,3 ом^-1-см²-экв^-1). Это, по-видимому, объясняется тем, что протон может переносится от молекулы к молекуле воды по так называемому «эстафетному» механизму

анод (+) | Н₃O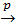⁺ Н₂O| катод (–).

В результате такого перескока протон проходит 0,86 А, что отвечает перемещению катиона гидроксония на 3,1 Ǻ, или перенос гидроксила в электрическом поле к аноду

анод (+) | Н₂O 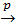ОН^– | катод (–),

при котором перескок протона вправо имеет следствием перемещение гидроксила влево. При этом гидроксил, принимающий протон, превращается в молекулу воды, а вместо него возникает новый анион, находящийся к аноду ближе, чем тот, который исчезает вследствие присоединения протона. Естественно, что при таком механизме проводимости подвижность ионов водорода и гидроксила значительно больше, чем ионов, которые просто дви­гаются в электрическом поле.

Дата добавления: 2014-01-03