Абсолютная и относительная производные

Сложное движение точки

Лекция 9

Краткое содержание: Сложное движение точки. Кинематические характеристики точки при сложном движении, абсолютное и относительное движения точки, переносное движение. Теорема о сложении скоростей. Теорема Кориолиса о сложении ускорений при сложном движении точки. Модуль и направление ускорения Кориолиса. Сложное движение тела. Сложение поступательных движений. Сложение вращательных движений. Сложение поступательного и вращательного движения тела.

Движение точки, рассматриваемое одновременно относительно нескольких систем координат, называется сложным движением.

Иначе говоря, сложным движением точки называется такое движение точки, которое может рассматриваться состоящим из нескольких движений.

При рассмотрении сложного движения точки необходимо рассматривать изменение векторных величин с течением времени по отношению к системам отсчета, движущимся друг относительно друга.

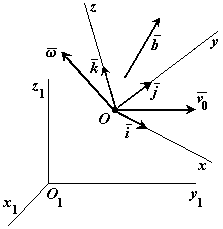Рассмотрим произвольный вектор 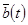в двух системах отсчета: подвижной и неподвижной. В подвижной системе отсчета только проекции вектора 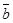являются функциями времени, в неподвижной системе отсчета кроме проекций, функциями времени являются и единичные вектора 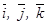(они изменяют свое направление в пространстве).

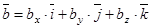(1)

Введем обозначения 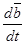- абсолютная производная – производная в неподвижной системе отсчета; 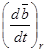- относительная производная – производная в подвижной системе отсчета.

Установим зависимость между абсолютной и относительной производными. Вычислим абсолютную производную по времени от вектора 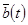используя формулу (1)

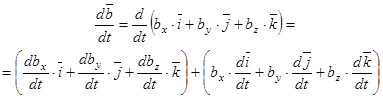(2)

Первые три слагаемых учитывают изменение вектора 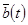при неизменных 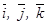и поэтому составляют относительную производную, т.е.

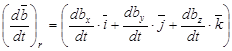. (3)

Производные по времени от единичных векторов определим по формулам Пуассона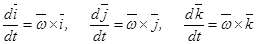

Вектор 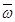- это угловая скорость вращательной части движения вокруг точки О подвижной системы отсчета относительно неподвижной.

После подстановки получаем

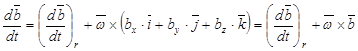. (4)

Получена формула зависимости производных вектора 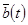в двух системах отсчета движущихся друг относительно друга (формула Бура).

Дата добавления: 2014-01-03; Просмотров: 1347; Нарушение авторских прав?; Мы поможем в написании вашей работы!