АЛГОРИТМ. 1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец)

расчета критерия c²

1. Занести в таблицу наименования разрядов и соответствующие им эмпирические частоты (первый столбец).

2. Рядом с каждой эмпирической частотой записать теоретическую частоту (второй столбец).

3. Подсчитать разности между эмпирической и теоретической частотой по каждому разряду (строке) и записать их в третий столбец.

4. Определить число степеней свободы по формуле:

- сопоставление эмпирического и теоретического распределения

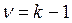, где k - количество разрядов признака

- сопоставление двух эмпирических распределений:

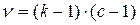, где k - количество разрядов признака,

с – количество сравниваемых распределений

Если 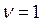, внести поправку на «непрерывность».

5. Возвести в квадрат полученные разности и занести их в четвертый столбец.

6. Разделить полученные квадраты разностей на теоретическую часто­ту и записать результаты в пятый столбец.

7. Просуммировать значения пятого столбца. Полученную сумму обо­значить как c²_эмп.

8. Определить по Табл. 7 Приложения 3 критические значения для данного числа степеней свободы ν.

Если c²_эмп меньше критического значения, расхождения между рас­пределениями статистически недостоверны.

Если c²_эмп равно критическому значению или превышает его, рас­хождения между распределениями статистически достоверны.

Пример 1. Сопоставление эмпирического распределения с теоретическим

Учительница 1 б класса, рассказывая студентам – практикантам о классе, сказала: «Весь класс сильный, дети готовы к школе, но Севка – на голову выше всех остальных. У него уже сформирована учебная позиция». Студенты - практиканты в случайном порядке выделили четырех детей, среди которых был и Сева. Используя карту наблюдения, студенты в течение 4 уроков наблюдали за этими детьми, регистрируя поведенческие реакции, сообщающие об активности и самостоятельности детей (см. Приложение 1). Можно ли считать, что по показателю активность упомянутый Сева действительно отличается от остальных детей?

Таблица 21.1.

Распределение реакций по показателям активность и самостоятельность

Дети	Сева	Леша	Вика	Оля	Всего
Активность
Самостоятельность

Действуем по алгоритму.

Шаг 2. Определим теоретическую частоту реакций, показывающих активность при равномерном распределении.

n – количество наблюдений, k – количество разрядов признака.

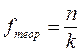, где

В нашем случае признак – показатели активности, разряды – дети.

.

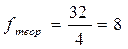Таблица 21.2.

Расчет критерия c²

Дети	Эмпирическая частота (fэ)	Теоретическая частота (fт)	(fэ - fт)	(fэ - fт)^2	(fэ - fт)^2/ fт
	Сева					4,500
	Леша			-3		1,125
	Вика
	Оля			-3		1,125
Суммы					6,750

Шаг 3. Подсчитаем разности между эмпирической и теоретической частотой. Все занесем в таблицу. Обратите внимание, сумма разностей между эмпирическими и теоретическими частотами обязательно должна быть равна нулю!

Шаг 4. Определим число степеней свободы

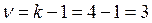
Шаг 5. Возведем полученные разности в квадрат.

Шаг 6. Разделим полученные квадраты разностей на теоретическую частоту.

Шаг 7. Просуммируем значения пятого столбца – получим c²_эмп. В нашем примере c²_эмп= 6,750.

Шаг 8. Определим критические значения c²_кр по Таблице 7 Приложения 3 для числа степеней свободы ν = 3.

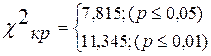
Ответ: Н₀ принимается. Распределение не отличается от равномерного и то, что Сева «на голову выше остальных» - всего лишь субъективное мнение учителя!

Пример 2. Сопоставление двух эмпирических распределений

Продолжая предыдущий пример, проверим, различаются ли между собой распределения поведенческих реакций по показателям активность и самостоятельность.

Для подсчета теоретических частот нам придется составить специальную таблицу (Таблица 21.3). Ячейки в двух столбцах слева обозначены буквами. Для каждой из них теперь будет подсчитана особая, только к данной ячейке относящаяся, теоретическая частота.

Теоретическая частота для каждой ячейки определяется по формуле:

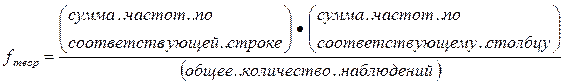
Таблица 21.3.

Эмпирические и теоретические частоты

Разряды - дети	Эмпирические частоты	Суммы	Теоретические частоты
Активность	Самост-ность	Активность	Самост-ность
	Сева		а		Б		13,65	а	15,35	Б
	Леша		В		Г		5,18	В	5,82	Г
	Вика		Д		Е		8,00	Д	9,00	Е
	Оля		Ж		З		5,18	Ж	5,82	З
Суммы

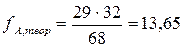
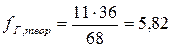
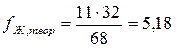
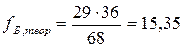
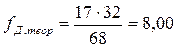
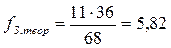
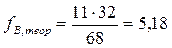
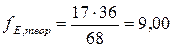
Для дальнейших расчетов нам удобнее сделать развертку таблицы 21.3 и действовать по алгоритму.

Таблица 21.4.

Расчет критерия c²

Ячейки таблицы частот	Эмпирическая частота (fэ)	Теоретическая частота (fт)	(fэ - fт)	(fэ - fт)^2	(fэ - fт)^2/ fт
	А		13,65	0,35	0,1225	0,009
	Б		15,35	-0,35	0,1225	0,008
	В		5,18	-0,18	0,0324	0,006
	Г		5,82	0,18	0,0324	0,006
	Д		8,00	0,00	0,00	0,00
	Е		9,00	0,00	0,00	0,00
	Ж		5,18	-0,18	0,0324	0,006
	З		5,82	0,18	0,0324	0,006
Суммы					0,041

Число степеней свободы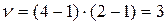

Определяем критические значения по Таблице 7 Приложения 3.

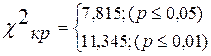
Ответ: Н₀ принимается. Распределения активности и самостоятельности у данных детей не различаются между собой.

Дата добавления: 2014-01-03