Выбор типа математической функции при построении уравнения регрессии

Практическое занятие №1

Лабораторная работа № 1

Задание. На основании данных табл. П1 для соответствующего варианта (табл. 2.3):

1. Построить уравнение линейной регрессии в стандартизированном мас­штабе.

2. Оценить информативность факторов на основе уравнения линейной регрессии в стандартизированном масштабе.

3. Вычислить частные коэффициенты корреляции.

4. Оценить их значимость при уровнях значимости 0,05 и 0,01.

5. Оценить информативность факторов на основе частных коэффициен­тов корреляции.

6. Построить уравнение регрессии с учетом только информативных фак­торов.

7. Проверить гипотезу о гомоскедастичности ряда остатков с уровнем зна­чимости а = 0,05.

Указания к решению. При выполнении лабораторной работы использо­вать возможности надстройки «Анализ данных» табличного процессора MS Ex­cel (для расчета корреляционной матрицы, нахождения уравнений регрессии, нахождения коэффициентов координации и др.).

Задание 2.

Для 13 клиентов спортивного отдела магазина зафиксирована сумма покупки х_t (в у. е.) и время разговора с продавцом y_t (в мин.). Данные представлены в табл. 2.1.

Таблица 2.1

хt

yt

Требуется:

1. Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная “длительность разговора с продавцом” объясняется переменной “величина покупки”.

2. Оценить с помощью МНК параметры линейного регрессионного уравнения, предположив, что переменная “величина покупки” объясняется переменной “длительность разговора с продавцом”.

3. Нарисовать диаграмму рассеяния величин (х_t, y_t) и обе линии регрессии. Объяснить, почему, если поменять экзогенную и эндогенную переменные местами, как правило, получаются различные уравнения регрессии.

Задание 3

Исследуется зависимость затрат на рекламу у от годового оборота х в некоторой отрасли. Для этого собрана информация по Т =20 случайно выбранным предприятиям этой отрасли о годовом обороте х_t и соответствующих расходах на рекламу y_t (в млн. руб.). Из выборки получены следующие данные: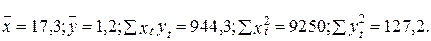

Предполагается, что зависимость y_t от х_t описывается следующим уравнением: y_t = a ₀+ a ₁ х_t + e_t (t =1,..., 20).

Требуется:

1. Оценить параметры a ₀ и a ₁ с помощью МНК.

2. Оценить дисперсию s_e ² “истинной” ошибки e_t.

3. Оценить дисперсии оценок a ₀ и a ₁ и их ковариацию.

Задание 4

Для данных задания 2.2 установлено, что “истинная” ошибка распределена нормально.

Требуется:

1. Определить 95%-е доверительные интервалы для параметров регрессии a ₀ и a ₁.

2. Проверить, можно ли утверждать, что с вероятностью 95% a ₀ Î K ₀ Ù a ₁ Î K ₁, где K ₀ и K ₁ – доверительные интервалы соответственно параметров a ₀ и a ₁, построенные в п. 1.

3. Определить 95%-й доверительный интервал для дисперсии “истинной” ошибки e_t.

Задание 5

Для анализа зависимости целевой переменной у от объясняющей переменной х получена выборка, состоящая из Т =50 наблюдений, и определены следующие показатели:

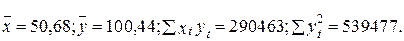
В основу исследования положена классическая линейная однофакторная модель нормальной регрессии y_t = a ₀+ a ₁ х_t + e_t (t =1,..., 50).

Требуется проверить следующие гипотезы:

1. H ₀¹: a ₁ ³ a ₁₀ =1 при уровне значимости a =0,05.

2. H ₀²: a ₀ £ a ₀₀ =50 при уровне значимости a =0,05.

3. H ₀³: s_e ² ³ s ₀ ² =25 при уровне значимости a =0,05.

Задание 6

Имеется нелинейное однофакторное уравнение регрессии

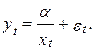
Требуется:

1. С помощью МНК оценить параметр регрессии a.

2. Рассмотреть линейное однофакторное уравнение y¢_t = a¢х_t + x_t, где y¢_t =1/ y_t и a¢ =1/ a, и установить, какое соотношение существует между случайными ошибками e_t и x_t.

3. С помощью МНК рассчитать оценку a¢ параметра регрессии a¢ и сравнить ее с оценкой из п. 1.

4. На основе трех пар наблюдений (х_t, y_t) – (4; 2,5); (2; 5); (10; 1;25) – показать, что оценки из пп. 1 и 3 в общем случае не совпадают.

Дата добавления: 2014-01-03