Применение эконометрических моделей

Проблемы идентификации.

1.Косвенный, двухшаговый и трехшаговый метод наименьших квадратов, общая схема алгоритма расчетов.

Алгоритм косвенного метода наименьших квадратов:

• Структурная модель преобразовывается в приведенную форму модели.

• Для каждого уравнения приведенной формы модели обычным МНК оцениваются приведенные коэффициенты.

• Коэффициенты приведенной формы модели трансформируются в параметры структурной формы модели.

Алгоритм двухшагового метода наименьших квадратов:

• Определяется приведенная форма модели, и находятся на ее основе оценки теоретических значений эндогенных переменных.

• Определяются структурные коэффициенты модели по данным теоретических (расчетных) значений эндогенных переменных. Косвенный МНК. Рассмотрим приведенную форму системы 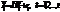, в которой 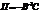переменные 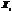-не мультиколлинеарны. роцедура статистического оценивания структурных параметров i-го уравнения: На 1-м этапе оцениваем с помощью обычного МНК все параметры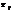 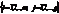приведенной формы. На 2-м этапе используются соотношения 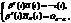связывающие структурные параметры i-го уравнения системы с параметрами 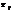приведенной формы. В случае точной идентифицируемости i-го уравнения структурной формы его параметры 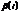и 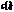однозначно определяются из системы по значениям 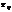. Подставив в эти соотношения вместо 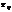их оценки 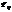и решив систему уравнений относительно 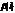и 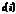, мы получим состоятельные оценк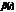и и 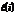структурных параметров i-го уравнения системы.

В случае неидентифицируемости анализируемого уравнения структурной формы число взаимно независимых связей между 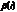, 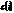и 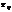будет меньше общего числа 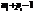неизвестных. Поэтому без дополнительной информации нельзя определить значения структурных коэффициентов 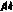и .

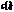Двухшаговый метод наименьших квадратов состоит в том, что оценивают параметры отдельного уравнения системы, а не рассматривают систему в целом. Двухшаговый метод наименьших квадратов (ДМНК) использует следующую центральную идею: на основе приведенной формы модели получают для сверхидентифицируемого уравнения теоретические значения эндогенных переменных, содержащихся в правой части уравнения. Затем они подставляются вместо фактических значений и применяют обычный МНК к структурной форме сверхидентифицируемого уравнения. В свою очередь, сверхидентифицируемая структурная модель может быть двух типов: либо все уравнения системы сверхидентифицируемы, либо же система содержит наряду со сверхидентифицируемыми и точно идентифицируемые уравнения. В первом случае, если все уравнения системы сверхидентифицируемые, для оценки структурных коэффициентов каждого уравнения используется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Дата добавления: 2014-01-03