Реологические свойства дисперсных ситем

Структурированные системы занимают промежуточное положение между жидкостью (жидкообразными телами) и твердым телом (твердообразными телами). В зависимости от различных факторов: концентрации, взаимодействия частиц дисперсной фазы и так далее, они могут проявлять как свойства жидкости, так и свойства твердого тела. Течение жидкообразных тел происходит при сколь угодно малых значениях предела текучести, то есть при Р_T = 0, а твердообразных - при Р_Т> 0. По значению Р_Т можно характеризовать реологию структурированных систем. Для них основным видом деформации является деформация сдвига.

Как известно, течение жидкообразных тел подчиняется закону Ньютона: напряжение сдвига пропорционально скорости деформации при сдвиге: 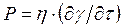, (9.3)

где h - вязкость жидкости; 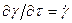- скорость деформации (изменение деформации во времени) или скорость течения жидкости.

Закон Ньютона можно сформулировать иначе: скорость деформации пропорциональна напряжению сдвига: .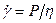

В уравнении (9.3) роль коэффициента пропорциональности играет вязкость (или внутреннее трение), которая является важнейшим свойством, характеризующим структуру любой дисперсной системы. Она является реологuческой константой и определяет способность жидкости сопротивляться течению. Величина, обратная вязкости 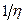, называется текучестью.

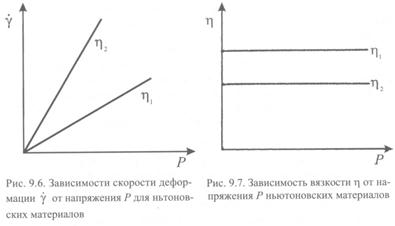
На рис. 9.6 представлены реологические кривые ньютоновских материалов с большей вязкостью h₁ и меньшей вязкостью - h₂. В координатах h- Р для тех же материалов получаются прямые, параллельные оси абсцисс (рис. 9.7).

Для течения идеальных жидкостей из капилляра Пуазейль предложил уравнение, которое является частным случаем уравнения Ньютона: 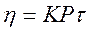, (9.4)

где K – постоянная капилляра;

P – давление течения;

t - время течения из капилляра.

Согласно (9.4) h не зависит от давления, так как с ростом Р во столько же раз уменьшается t.

По законам Ньютона и Пуазейля вязкость не должна зависеть от внешнего давления только в ламинарном потоке. В условиях турбулентности вязкость начинает увеличиваться с ростом давления, и основные законы вязкого течения оказываются не применимыми.

Вязкость дисперсных систем отличается от вязкости дисперсионной среды за счет заполнения части растворителя дисперсной фазой. Вязкость таких систем растет по мере увеличения концен­трации дисперсной фазы. Если концентрация дисперсной фазы невелика и столкновение частиц исключается, то для определения вязкости можно пользоваться формулой Эйнштейна:

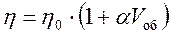, (9.5)

где h, h₀- вязкость дисперсной системы и дисперсионной среды;

a - коэффициент, учитывающий форму частиц (для сферических частиц a = 2,5);

V _об - объемная концентрация дисперсной фазы ().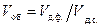

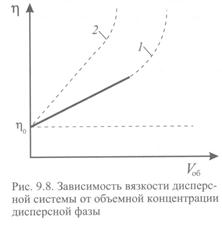
В соответствии с уравнением (9.5), вязкость дисперсной системы увеличивается по мере увеличения объемной концентрации(рис. 9.8, кривая 1). Формула (9.5) справедлива, если концентрация дисперсной фазы не превышает 6 %. При увеличении V _об до 30 % можно пользоваться формулой, которая отличается от уравнения Эйнштейна последним членом:

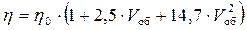(9.6)

Из уравнения (9.6) видно, что, по мере увеличения концентрации дисперсной фазы линейная зависимость h - V _об нарушается в условиях взаимного столкновения частиц, однако при данной концентрации вязкость остается постоянной. Подобные системы, подчиняющиеся уравнениям Ньютона, Пуазейля и Эйнштейна, называются нормальными или ньютоновскuми.

Для структурированных систем наблюдается отклонение от теоретической зависимости уже при малых концентрациях (рис. 9.8, кривая 2). Они не подчиняются законам Ньютона, Пуазейля и Энштейна и называются аномальными или неньютоновскими.

Такое деление на ньютоновские и неньютоновские материалы не совсем верно, так как часть деформации любого материала может быть описана уравнением Ньютона.

Правильнее деление текучих материалов на ньютоновские и неньютоновские проводить по признаку зависимости или независимости вязкости h от напряжения сдвига Р. По сравнению с обычными (неструктурированными) жидкостями, структурированные системы обладают повышенной вязкостью, хотя вязкость и не является критерием структурообразования. Например, вязкость плазмы крови, являющейся структурированной системой, ниже, чем глицерина, не образующего структур.

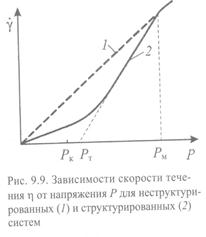
Наличие структуры изменяет характер течения жидкости. Поэтому исследование кривых зависимости скорости течения 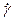от приложенного внешнего напряжения Р позволяет изучать структурообразование в системе (рис. 9.9). Для чистых бесструктурных жидкостей между 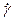и Р наблюдается линейная зависимость (кривая 1) с постоянным наклоном, соответствующим постоянной вязкости h. Для структурированных - характерны кривые типа 2 с переменной вязкостью h, зависящей от Р. При малых напряжениях (Р < Р _т ) наблюдается медленное течение с малым наклоном. Это течение происходит при большой вязкости системы, соответствующей неразрушенной структуре, и называется ползучестью. Далее идет возрастание скорости течения, соответствующее разрушению структуры. Вязкость системы снижается, а скорость движения системы увеличивается. Для этого случая кривая описывается уравнением Бингама, которое отличается от уравнения Ньютона (9.2) и (9.3) на величину Р_Т - предела текучести:

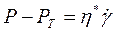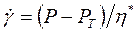или (9.7)

Чем прочнее структура, тем выше предел текучести. Величина Р_Т находится экстраполяцией этой части кривой к оси напряжений и характеризует усилие, необходимое для начала разрушения структуры. Дальнейшее увеличение напряжения вызывает полное разрушение структуры при Р=Р _м Величина Р _м называется предельным напряжением сдвига. Конечный участок кривой течения отвечает закону Ньютона с меньшей вязкостью.

Часто кривые течения имеют другой вид. Они начинаются при Р = Р_к, то есть при Р < Р _к течение вообще отсутствует. Такие кривые характерны для твердообразных систем. При Р = Р_к система начинает течь при неразрушенной структурной сетке. В интервале Р _т - Р _м структура разрушается.

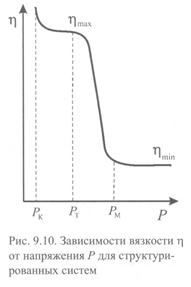
Зависимость, представленная на рис. 9.9, называется полной реологической кривой течения дисперсной системы. Она может быть представлена также в координатах вязкость-напряжение сдвига (рис. 9.10). Вязкость неструктурированных систем является величиной постоянной и не зависит от внешнего воздействия. Структурированные системы обладают аномальной вязкостью. Для них вязкость является величиной переменной и изменяется от максимального значения до минимального в интервале от Р _т до Р _м. С увеличением внешнего воздействия происходит нарушение, а затем полное разрушение структуры системы. Этот процесс сопровождается уменьшением вязкости. Когда структура полностью разрушается, вязкость достигает минимальной величины.

Свойства структурированных систем могут быть охарактеризованы тремя величинами вязкости: ньютоновской - для неразрушенной структуры h_max, ньютоновской - для предельно разрушенной структуры h_min и пластической вязкостью h* в промежуточной области (рис. 9.10), где вязкость переменная: 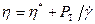. Прочность структуры можно оценить разностью 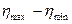. Чем больше эта разность, тем прочнее структура. Значения h_max и h_min могут различаться на несколько порядков.

Если тело обладает тиксотропными свойствами, то после снятия нагрузки в нем возобновляется структура, вязкость системы при этом возрастает, а сама система относится к псевдопластической. Иногда действие механической нагрузки приводит не к разрушению, а, наоборот, к образованию контактов между частицами и увеличению ее вяз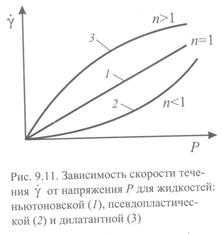кости. Например, при сбивании сливочного масла. Это явление обратное тиксотропии носит название реопексии.

Известен иной тип реологических кривых, где скорость деформации с увеличением напряжения растет медленнее, чем по линейному закону. Такие материалы называются дuлатантными (рис. 9.11). Они определяются эмпирической зависимостью Оствальда-Вейля, которая является обобщением закона Ньютона: 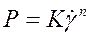, (9.8)

где К и п - эмпирические константы, отражающие свойства материала.

При п = 1, К = h и уравнение (9.8) превращается в уравнение Ньютона (9.3). Отклонение величины п от 1 характеризует степень отклонения свойств неньютоновских жидкостей от ньютоновских. Для ползучих (псевдопластических) материалов п < 1, а для дилатантных п > 1, т. е. в первом случае вязкость уменьшается с ростом Р, а во втором возрастает (рис. 9.11).

Измерение вязкости дисперсных систем, в зависимости от скорости течения, широко используется на практике. В технологическом процессе на различных его стадиях вязкость структурированных дисперсных систем может сильно изменяться. В ряде случаев, например, при транспортировке, необходимо, чтобы продукт имел максимальную вязкость, то есть был структурированным, а для перекачки продукта, напротив, нужно создавать такую скорость течения, которая бы соответствовала его минимальной вязкости.

Вязкость коллоидной системы зависит от

· концентрации дисперсной фазы,

· природы дисперсионной среды и дисперсной фазы,

· наличия стабилизатора.

Вязкость жидкости – это сопротивление передвижения одного слоя жидкости относительно другого слоя.

Единица вязкости – Пуаз, он характеризует жидкости, в которых слои в одном квадратном сантиметре на расстоянии одного сантиметра движутся относительно друг друга со скоростью одного сантиметра в секунду под действием силы в одну дину 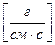или 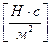. Если при изменении скорости течения в пределах ламинарности вязкость жидкости остается постоянной, т.е. скорость течения прямо пропорциональна приложенной к жидкости силе, то жидкости называются ньютоновскими. Если условие не выполняется, значит, жидкости называются неньютоновскими. Чистые жидкости и разбавленные растворы коллоидов со сферическими частицами характеризуется как ньютоновские жидкости, тогда как растворы коллоидов с палочкообразными или нитевидными частицами обладают неньютоновской вязкостью. Все коллоидные растворы имеют вязкость, превышающую вязкость дисперсионной среды. Для коллоидных систем, движущихся ламинарно и имеющих дисперсную фазу в виде шарообразных частиц, не имеющих межмолекулярного взаимодействия, вязкость описывается уравнением Эйнштейна

,

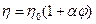где  - объемная концентрация дисперсной фазы;

_ - динамическая вязкость дисперсионной среды;

 - коэффициент, зависящий от формы частиц.

Видоизменив, получим:

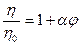- относительная вязкость

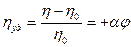- удельная вязкость = h_отн-1

Из уравнения следует, что:

1) h пропорциональна концентрации дисперсной фазы;

2) h_{дисп. сист.}>h_{дисп. ср.}

Для концентрированных систем уравнение Эйнштейна неприменимо. Это объясняется целым рядом причин:

1. В жидкости около частиц возникает макропоток, затрудняющий движение системы;

2. Сольватация частиц. Оно проявляется в увеличении объема частиц за счет адсорбции дисперсионной среды;

3. Проявление сил отталкивания между частицами, несущими одинаковые заряды. Смолуховский показал, что h_{заряженных частиц} больше, чем h_{незаряженных}.

,

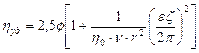где h₀ – вязкость среды;

n - удельная электропроводность;

r - радиус частиц;

z - дзета-потенциал;

e - диэлектрическая проницаемость.

Структурная вязкость - вязкость структурированных систем, т.е. систем, где наблюдается явная тенденция образования пространственных молекулярных сеток между частицами дисперсной фазы. Они не подчиняются закону Ньютона и в случае образования структуры течение системы начинается лишь тогда, когда напряжение сдвига Р превысит какое-либо критическое значение P_T, необходимое для разрушения структуры, т.е. когда начинает выполняться условие Р > P_T. Такое течение Бингам назвал пластическим, а критическое напряжение сдвига (предельное) – пределом текучести.

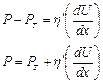- уравнение Бингама,

где ^ - вязкость, отвечающая пластическому течению системы или пластическая вязкость;

dU/dx – градиент скорости.

Теория Эйнштейна была использована Штаудингером для установления формулы вязкости разбавленных растворов полимеров. Для растворов, содержащих палочкообразные макромолекулы, должно соблюдаться соотношение

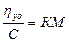, где 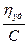приведенная вязкость; h_уд = КМС

Удельная вязкость прямо пропорциональна концентрации и молекулярной массе полимера; К определяют независимым методом, например, по растворам полимеров с известной молекулярной массой М. Она зависит от данного гомологического ряда и растворителя; С – массовая концентрация полимера.

Уравнение справедливо лишь для полимеров с короткими жесткими цепями, которые могут сохранять палочкообразную форму. Гибкие молекулы с длинными цепями, обычно свертываются в клубок, что уменьшает сопротивление движению. При этом К изменяется и зависимость становится нелинейной.

Широкое распространение для определения молекулярной массы полимера с гибкими и длинными макромолекулами получило уравнение Марка-Куна-Хаувинка:

[h]= КМ^а,

где К и а – постоянные для данного гомологического ряда и растворителя.

Для разбавленных растворов, полимеров широко используется зависимость удельной вязкости от концентрации.

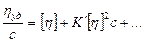- уравнение Хаггинса,

включающая константу К^/, которая характеризует взаимодействие полимера с растворителем. Чем хуже растворитель, тем выше значения К^/. Формула удобна для экстраполяции [h] при бесконечном разбавлении.

[h]- характеристическая вязкость, она оценивает прирост вязкости раствора, вызванный наличием макрочастиц и их вращений.

.

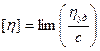Рассмотрим три наиболее распространенных метода измерения вязкости:

1. Капиллярный метод (вискозиметр Оствальда).

В специальный капилляр заливают определенный объем жидкости V (см³) и она вытекает под давлением Р (дин/см²) в течение времени t(сек), высота l и радиус r. Пуазейль показал:

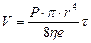, где h - коэффициент вязкости.

Чаще проводят сравнительное определение вязкости. Для этого измеряют время истечения t и t₁ одинаковых объемов испытуемой и стандартной жидкости, тогда

,

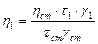где g - плотность.

Дата добавления: 2014-01-03