Формальные языки и грамматики. Основные термины и определения

Алфавит – конечное непустое множество символов.

Термин символ следует понимать здесь в самом широком смысле слова. Символом можно считать любой знак или совокупность знаков, рассматриваемую как нечто неделимое (буква, цифра, знак препинания, служебное слово, иероглиф и т.д.).

Будем обозначать алфавит символом 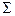(sigma). Т.к. алфавит – это множество, поэтому при перечислении его элементов используются фигурные скобки.

Примеры алфавитов:

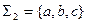
Под 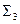подразумевается алфавит языка Паскаль.

Цепочка над алфавитом 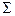- произвольная конечная последовательность символов из .

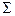Примеры цепочек над алфавитом :

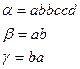
Цепочки будем обозначать греческими буквами.

Характеристикой цепочки является ее длина. Длиной цепочки называется число символов, образующих цепочку. Длина цепочки 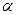равна 9 и обозначается |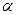

Пустая цепочка – цепочка, не содержащая символов (содержащая ноль символов). Обозначается буквой 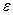(epsilon).

Если 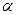и цепочки, то запись 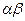означает их конкатенацию (слияние).

Если 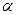- цепочка, то запись 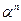означает цепочку, образованную n-кратным повторением цепочки :

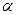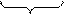
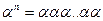
n-раз

Будем обозначать

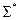- бесконечное множество всех цепочек над алфавитом 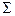, включая пустую цепочку,

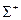- множество всех цепочек над алфавитом 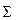, не включая пустой цепочки.

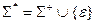
Например, если , 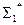представляет собой множество всех цепочек, которые могут быть составлены из символов 0 и 1, включая пустую цепочку:

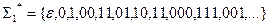
Языком над алфавитом 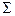называется произвольное множество цепочек, составленных из символов .

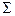Принадлежащие языку цепочки называют также предложениями языка.

Отметим, что множество цепочек 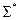всегда бесконечно, в то время как множество цепочек, образующих язык может быть конечным.

5 Порождающие грамматики (Грамматики Н.Хомского [1])

Порождающие грамматики – мощный механизм, позволяющий задавать множество правил вывода, порождающих цепочки над 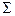, принадлежащие языку L.

Порождающей грамматикой называется четверка:

G=(T, N, P, S)

Где

Т – конечное множество терминальных (основных) символов- основной алфавит. Элементами множества Т являются символы, из которых в конечном итоге и состоят цепочки языка, порождаемые грамматикой. Т – это не что иное, как алфавит языка, порождаемого грамматикой. В дальнейшем терминалы будем обозначать малыми латинскими буквами a, b, c,.. и. т.д;

N - конечное множество нетерминальных (вспомогательных) символов – вспомогательный алфавит. Нетерминалы – это понятия грамматики (языка), которые используются при его описании. Нетерминалы будем обозначать заглавными латинскими буквами A, B, C, …;

Р – конечное множество правил вывода, называемых также продукциями. Каждое правило множества имеет вид: 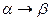, ( символ «®» читается как «это есть» )

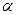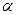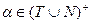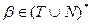где и - цепочки терминальных и нетерминальных символов. Цепочка не должна быть пустой, цепочка может быть пуста: ; . Правило вывода определяет возможность подстановки вместо 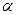в процессе вывода (порождения) цепочек языка;

S (S Î N) - начальный символ грамматики – один из множества нетерминальных символов, начальный нетерминал. Начальный нетерминал – это понятие грамматики, соответствующее правильному предложению языка.

Дата добавления: 2014-01-03