Математические модели

Создание математических моделей параметров НЭМП — сложная задача, особенно для помех негауссового типа. Многие математические модели основаны на эмпирических моделях, разработанных по результатам статистических измерений параметров помех. Степень аппроксимации математической модели проверяется по эмпирической модели путем опенки математического ожидания М и среднеквадратического отклонения от исследуемого параметра Ui помехи в пределах диапазона его измерения:

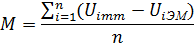
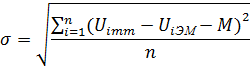
где 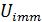- значение параметра, соответствующее математической модели; 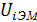- значение параметра, соответствующее эмпирической модели; 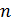- число точек характеристик, по которым определяется расхождение данных.

Однако эмпирическая модель отражает частный случай, относящийся к конкретному источнику (виду) помехи, и может не соответствовать общей закономерности. Более перспективным подходом является создание канонических моделей (подход Миддлтона), т. е. таких моделей, которые выражают основные закономерности и независимы от особенностей конкретного источника помехи с его количественными параметрами и, следовательно, являются обобщающими [68].

Согласно данному подходу все виды помех, в том числе импульсные, делит на три класса:

класс А— узкополосная помеха, полоса частот которой не превышает полосы пропускания приемника и широкополосная помеха при условии, что она когерентная, т. е. импульсная регулярная (например, импульсы РЛС), и, во-вторых, удовлетворяет неравенству D_fr*T_n»1, где D_fr— эффективная полоса пропускания линейного ВЧ тракта приемника и TN — длительность когерентного импульса. Это неравенство подразумевает, что в узкополоснои приемнике эффекты нестационарных процессов незначительны.К этому классу относят также некогерентную импульсную широкополосную помеху с малой длительностью импульса относится к классу Вив отличие от когерентной отвечает условию D_fr*T_n=1 (или даже D_fr*T_n<<1);

класс В—широкополосная помеха;

класс С — помеха в виде сочетания помех класса А и класса В. При этом предполагается, что помеха класса А не приводит к возникновению нестационарных процессов во входном тракте и после преобразователя частоты приемника, являющегося линейным по отношению к помехе. Наоборот, помеха класса В создает нестационарные процессы в приемнике, который по отношению к помехе находится как бы под «ударным возбуждением».

В моделях Миддлтона используются две категории параметров: параметры, общие для всех канонических моделей данного класса, и параметры, характерные для тех эмпирических моделей, которые связаны с каноническими моделями этого класса.

Если для некоторой канонической модели общие параметры определены, то характерные параметры могут быть определены или уточнены из этой эмпирической модели. В моделях помех класса А имеется 3 общих и 3 характерных параметра, в моделях класса В соответственно по 6 параметров. Описанные в литературе канонические модели обоих классов и особенно класса В сложны и пока не получили широкого распространения.

Подход Миддлтона к построению моделей базируется на анализе действия помех на приемное устройство и имеет целью изыскать возможности снижения его восприимчивости к помехам.

Дата добавления: 2014-01-03