Алгоритмические задачи

Задача о четырех красках.

Задача о кенигсбергских мостах.

Задачи, послужившие основой теории графов.

На рис. 6 схематически изображена карта города Кенигсберга, относящаяся к XVIII в. Город был расположен на берегах и двух островах реки Преголи. Острова между собой и с берегами были связаны семью мостами. Жители города любили размышлять над проблемой: можно ли, выйдя из дома, вернуться обратно, пройдя по каждому мосту только один раз?

Полностью неориентированный граф 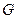, отвечающий задаче, представлен на рис. 7. Вершины 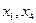соответствуют правому и левому берегам реки, вершины 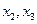- островам, ребра графа — мостам. На языке графов, задача формулируется следующим образом: существует ли в графе простой цикл, содержащий все ребра (эйлеров цикл).

Л. Эйлер сформулировал и доказал необходимое и достаточное условие того, чтобы в произвольном полностью неориентированном связном графе существовал эйлеров цикл.

Теорема 1: Эйлеров цикл в симметрическом связном графе 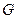существует тогда и только тогда, когда степени всех его вершин — четные числа.

Доказательство: Необходимость условия теоремы очевидна, поскольку при каждом проходе через вершину, используются ровно два ребра.

Достаточность можно доказать индукцией по числу ребер графа. При числе ребер, равном двум, как нетрудно видеть, теорема справедлива. Пусть утверждение теоремы верно для всех графов с числом ребер, непревосходящем числа 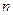. Для графа с числом ребер 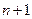рассмотрим произвольный простой цикл. Хотя бы один такой цикл обязательно существует для графов с четными степенями вершин. Если в графе не имеется ни одного простого цикла, то любое его ребро — перешеек. Удаляя какое-либо ребро графа, инцидентное, скажем, вершинам 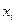и 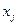, разбиваем граф на две компоненты связности. Каждое ребро в этих компонентах связности — также перешеек. После удаления ребра степени вершин 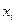и 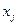стали нечетными. Склеим компоненты связности по вершинам 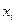, и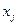. Новая вершина, как и все остальные, в полученном связном графе имеет четную степень. Число ребер в получившемся графе равно 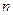. По предположению индукции в нем существует эйлеров цикл. Но это противоречит предположению, что в каждой компоненте связности все ребра — перешейки. Если рассматриваемый простой цикл 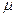содержит все ребра, то теорема доказана. В противном случае найдутся вершины 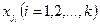, принадлежащие парам смежных ребер цикла, такие, что из каждой исходит по крайней мере одно ребро, не входящее в построенный цикл. В силу условия теоремы число ребер, исходящих из вершины 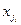и не принадлежащих циклу 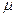, обязательно четно.

Например, в графе, изображенном на рис. 8,:имеем:

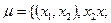
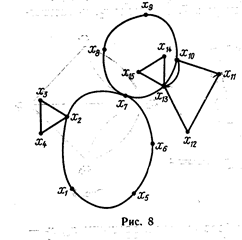
где 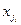есть вершины , , .

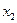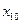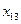Рассмотрим подграф 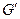графа 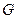, построенный с помощью ребер, не входящих в цикл 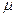. Подграф 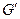состоит, быть может, из нескольких компонент связности. Степени всех вершин 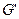— четные числа. Каждая компонента связности 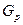подграфа 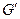удовлетворяет предположению индукции, так как содержит меньше, чем 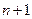ребро. Следовательно, в каждой компоненте 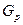существует; эйлеров цикл, содержащий, по крайней мере, одну из вершин 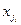. Присоединяя к циклу 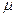эйлеровы циклы подграфов 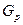, получаем эйлеров цикл графа .

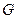Формулировка этой задачи чрезвычайно проста и не соответствует всей глубине и сложности проблемы: можно ли на любой политико-административной карте раскрасить страны так, чтобы никакие две страны, имеющие общую границу, не были раскрашены одинаковой краской, и чтобы были использованы всего четыре краски? Уточним, что если две страны граничат по точке, то они не считаются имеющими общую границу.

В терминах теории графов задача может быть поставлена следующим образом. Дан произвольный полностью неориентированный плоский граф 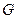. Можно ли каждую вершину графа 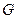раскрасить с помощью одной из четырех красок так, чтобы никакие две смежные вершины (вершины, соединенные хотя бы одним ребром) не были раскрашены в один цвет. Конечно, нетрудно привести примеры графов, которые раскрашиваются в одну, две, три или четыре краски. В §6 будет доказана теорема о том, что любой плоский граф может быть раскрашен с помощью пяти красок. Тем не менее, проблема четырех красок до сих пор не решена. Удалось лишь доказать, что такую раскраску можно осуществить для всех плоских графов с числом вершин, не превосходящим 38.

Задача эта приобрела известность с 1878 г., когда английский математик Кэли привел ее формулировку на заседании английского королевского научного общества; добавив, что не мог ее решить, хотя и размышлял над ней длительное время. С тех пор многие выдающиеся математики пробовали свои силы в решении этой задачи. Удивительно, что для графов, нарисованных на торе, листе Мёбиуса или бутылке Клейна, соответствующая задача решена, т. е. установлено необходимое и достаточное число красок для раскрашивания.

Дата добавления: 2014-01-03