Алгоритм решения

1°. Присвоить вершине 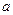метку 0.

2°. Есл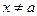и и 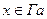, то присвоить каждой такой вершине метку 1.

3°. Пусть 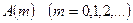— множество вершин, имеющих метку 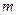. Вершинам множества 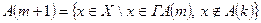при 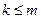присвоить метку .

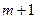4°. Процесс присвоения вершинам меток прекратить, как только вершина 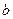получит некоторую метку .

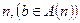5°. Рассмотреть вершины 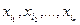, такие, что

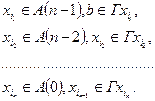
Замечание: Если на некотором шаге невозможно присвоение метки от значения 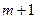вершинам в силу того, что множество 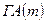пусто, и вершина 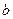не получила метки, то это означает, что в графе 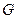не существует никакого пути, соединяющего вершину 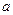с вершиной .

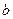Доказательство того, что применение правил алгоритма всегда приводит к решению задачи 1, основывается на том очевидном факте, что вершины множества 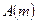— это все те вершины, в которые можно попасть из вершины 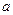по путям, содержащим ровно 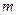дуг, и нельзя попасть по пути длины меньшей, чем .

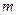2. Путь кратчайшей длины. Рассмотрим теперь случай, когда каждой дуге 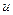графа 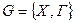сопоставлено положительное число 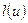. Это число 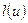можно назвать длиной дуги. Длиной пути 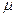назовем сумму длин дуг, входящих в путь :

.

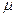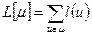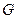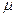Возникает следующая задача. Найти в графе путь кратчайшей длины, соединяющий вершину 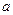с вершиной .

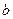Алгоритм решения.

1°. Перенумеровать вершины графа 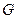так, чтобы вершина 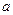получила номер 0. Обозначить вершину 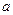через 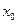. (При этом вершина 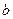совпадет с некоторой вершиной ).

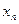2°. Присвоить каждой вершине 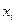метку 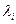так, чтобы 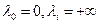при .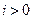

3°. Найти такую дугу 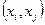, для которой 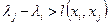. (Полагаем, что 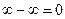.) У вершины 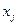заменить метку 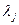на новую, меньшую метку .

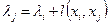4°. Применять правило 3° до тех пор, пока для каждой дуги 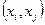не станет справедливым неравенство: .

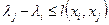5 °. Во множестве 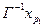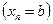найти такую вершину 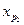, что .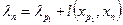

Аналогично, во множестве найти такую вершину 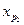, чтобы было справедливо равенство 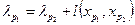и т. д.

После некоторого числа шагов вершина 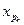совпадет с вершиной .

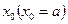Путь 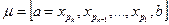— кратчайший, его длина равна .

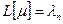Дата добавления: 2014-01-03