Метод Монжа

Образование чертежа точки в системе двух и трех плоскостей проекций

Данный метод позволяет определить место каждой точки изображения относительно других точек.

Точку (предмет) помещают в систему двух взаимоперпендикулярных плоскостей, которые используются в качестве плоскостей проекций.

П₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

х – ось проекций: х = П1 ∩ П2.

Плоскости проекций П₁, П₂ делят пространство на четыре части, называемые четвертями. Точка А находится в I четверти пространства. Проведя перпендикуляры к П₁ (A Î s’ ┴ П₁, A₁ = s’ ∩ П₁) и П₂ (A Î s” ┴ П₂, A₂ = s” ∩ П₂), получаем проекции точки А (рис.4):

А₁ – горизонтальная проекция точки А,

А₂ – фронтальная проекция точки А.

Если даны проекции А₁ и А₂ некоторой точки А, то проведя перпендикуляры: через т. А₁ к плоскости П₁ (s’ ┴ П₁), а через т. А₂ к П₂ (s” ┴ П₂), получим в пересечении этих прямых определенную точку А (s’ ∩ s” = A) (рис.5).

Рис.4 Рис.5

Вывод: Две проекции точки вполне определяют ее положение в пространстве относительно данной системы плоскостей проекций.

Вращением вокруг оси Ох плоскость П₁ совместим с плоскостью П₂. При этом проекции А₂ и А₁ точки А расположатся на одном перпендикуляре к оси проекций – на линии связи.

Рис.6

В результате указанного совмещения плоскостей П₂ и П₁ получается чертеж, известный под названием эпюр Монжа или двухкартинный чертеж, включающий две взаимосвязанные проекции - “картины”. Это чертеж в системе П₁, П₂ или в системе двух прямоугольных проекций. Условимся в дальнейшем двухкартинный чертеж, а также чертеж, в основе которого лежит метод Монжа, называть одним словом – чертеж и понимать это только в указанном смысле. В других случаях применения слова «чертеж» оно будет сопровождаться соответствующим определением (перспективный чертеж, аксонометрический чертеж и т.п.).

Известно, что чертежи сложных конструкций содержат не две, а большее число изображений – проекций. Рассмотрим введение в систему П₁, П₂ еще одной плоскости проекций, перпендикулярной П₁ и П₂ (рис.7):

П₃ – профильная плоскость проекций;

х = П₁ ∩ П₂; у = П₁ ∩ П₃; z = П₂ ∩ П₃; О = х ∩ у ∩ z.

Опустим перпендикуляр на плоскость П₃ из точки А и получим:

А₃ – профильную проекцию точки А (рис.8)

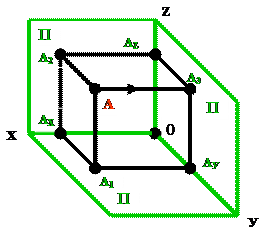
Рис.7 Рис.8

Для получения трехкартинного чертежа точки надо повернуть плоскость П₁ вокруг оси x и плоскость П₃ вокруг оси z до совмещения их с плоскостью П₂ (рис.9).

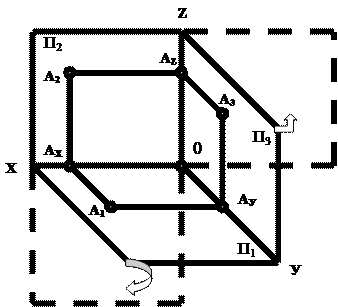
Рис.9

Выводы:

1. Каждая точка пространства характеризуется тремя координатами: А (х, у, z).

2. Каждая проекция точки на чертеже – двумя координатами: А₁ (х, у); А₂ (х, z); А₃ (у, z).

3. Две проекции точки однозначно определяют ее положение в пространстве.

Дата добавления: 2014-01-03