Апериодическое звено

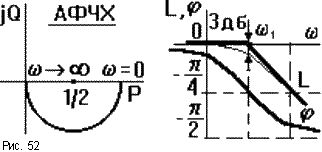
При k = 1 получаем следующие выражения ЧХ:

W(p) = ;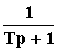

;

;

;

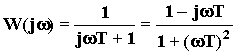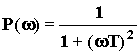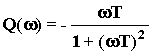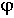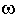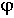() = 1 - 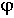2 = - arctg(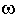T);

;

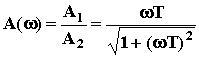L(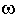) = 20lg(A(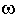)) = - 10lg(1 + (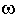T)2).

Здесь A1 и A2 - амплитуды числителя и знаменателя ЛФЧХ; 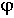1 и 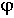2 - аргументы числителя и знаменателя. ЛФЧХ:

ЧХ показаны на рис.52. АФЧХ есть полуокружность радиусом 1/2 с центром в точке P = 1/2. При построении асимптотической ЛАЧХ считают, что при 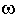< 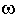₁ = 1/T можно пренебречь (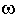T)² выражении для L(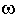), то есть L(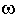) 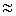- 10lg1 = 0.. При 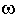>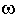₁ пренебрегают единицей в выражении в скобках, то есть L(w) 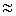- 20lg(wT). Поэтому ЛАЧХ проходит вдоль оси абсцисс до сопрягающей частоты, затем - под наклоном - 20 дб/дек. Частота w1 называется сопрягающей частотой. Максимальное отличие реальных ЛАЧХ от асимптотических не превышает 3 дб при 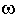= 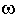₁.

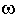ЛФЧХ асимптотически стремится к нулю при уменьшении w до нуля (чем меньше частота, тем меньше искажения сигнала по фазе) и к - /2 при возрастании до бесконечности. Перегиб в точке 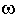= 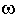₁ при 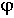(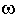) = - /4. ЛФЧХ всех апериодических звеньев имеют одинаковую форму и могут быть построены по типовой кривой с параллельным сдвигом вдоль оси частот.

Дата добавления: 2014-01-03